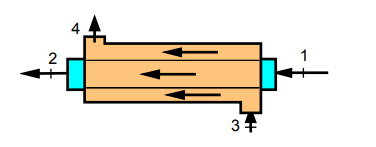
A coflowing (same direction) heat exchanger has one line with 0.5 lbm/s oxygen at 68 F and 30 psia entering and the other line has 1.2 lbm/s nitrogen at 20 psia and 900 R entering. The heat exchanger is long enough so that the two flows exit at the same temperature. Use constant heat capacities and find the exit temperature and the second law efficiency for the heat exchanger assuming ambient at 68 F.
C.V. Heat exchanger, steady 2 flows in and two flows out.
Energy Eq.4.10: \dot{ m }_{ O 2} h _{1}+\dot{ m }_{ N 2} h _{3}=\dot{ m }_{ O 2} h _{2}+\dot{ m }_{ N 2} h _{4}
Same exit tempearture so T _{4}= T _{2} with values from Table F.4
\dot{ m }_{ O 2} C _{ P O 2} T _{1}+\dot{ m }_{ N 2} C _{ P N 2} T _{3}=\left(\dot{ m }_{ O 2} C _{ P O 2}+\dot{ m }_{ N 2} C _{ P N 2}\right) T _{2}T _{2}=\frac{0.5 \times 0.22 \times 527.7+1.2 \times 0.249 \times 900}{0.5 \times 0.22+1.2 \times 0.249}=\frac{326.97}{0.4088}= 8 0 0 R
The second law efficiency for a heat exchanger is the ratio of the exergy gain by one fluid divided by the exergy drop in the other fluid. For each flow exergy is Eq.8.23 include mass flow rate as in Eq.8.38
For the oxygen flow:
\begin{aligned}\dot{m}_{ O 2}\left(\psi_{2}-\psi_{1}\right) &=\dot{ m }_{ O 2}\left[ h _{2}- h _{1}- T _{ o }\left( s _{2}- s _{1}\right)\right] \\&=\dot{ m }_{ O 2}\left[ C _{ P }\left( T _{2}- T _{1}\right)- T _{ o }\left[ C _{ P } \ln \left( T _{2} / T _{1}\right)- R \ln \left( P _{2} / P _{1}\right)\right]\right.\\&=\dot{ m }_{ O 2} C _{ P }\left[ T _{2}- T _{1}- T _{ o } \ln \left( T _{2} / T _{1}\right)\right] \\&=0.5 \times 0.22[800-527.7-536.7 \ln (800 / 527.7)]=5.389 Btu / s\end{aligned}For the nitrogen flow
\begin{aligned}&\dot{ m }_{ N 2}\left(\psi_{3}-\psi_{4}\right)=\dot{ m }_{ N 2} C _{ P }\left[ T _{3}- T _{4}- T _{ o } \ln \left( T _{3} / T _{4}\right)\right] \\&=1.2 \times 0.249[900-800-536.7 \ln (900 / 800)]=10.992 Btu / s\end{aligned}From Eq.8.32
{\eta_{2^{nd }} }_{ Law }=\frac{\dot{ m }_{ O 2}\left(\psi_{1}-\psi_{2}\right)}{\dot{ m }_{ N 2}\left(\psi_{3}-\psi_{4}\right)}=\frac{5.389}{10.992}= 0 . 4 9…………………………………….
Eq.4.10 : \dot{Q}_{ C.V. }+\sum \dot{m}_{i}\left(h_{i}+\frac{ V _{i}^{2}}{2}+g Z_{i}\right)=\sum \dot{m}_{e}\left(h_{e}+\frac{ V _{e}^{2}}{2}+g Z_{e}\right)+\dot{W}_{ C . V. }
Eq.8.23 :
\psi_{i}-\psi_{e}=\left[\left(h_{\text {tot } i}-T_{0} s_{i}\right)-\left(h_{0}-T_{0} s_{0}+g Z_{0}\right)\right]-\left[\left(h_{\text {tot } e}-T_{0} s_{e}\right)-\left(h_{0}-T_{0} s_{0}+g Z_{0}\right)\right]=\left(h_{\text {tot } i}-T_{0} s_{i}\right)-\left(h_{\text {tot } e}-T_{0} s_{e}\right)
Eq.8.38 :
\frac{d \Phi}{d t}=\sum\left(1-\frac{T_{0}}{T}\right) \dot{Q}_{ c.v . } Transfer by heat at T
-\dot{W}_{ c.v. }+P_{0} \frac{d V}{d t} Transfer by shaft/boundary work
+\sum \dot{m}_{i} \psi_{i}-\sum \dot{m}_{e} \psi_{e} Transfer by flow
-T_{0} \dot{S}_{ gen } Exergy destruction
Eq.8.32 : \eta_{2nd law }=\frac{\dot{m}_{1}\left(\psi_{2}-\psi_{1}\right)}{\dot{m}_{3}\left(\psi_{3}-\psi_{4}\right)}
