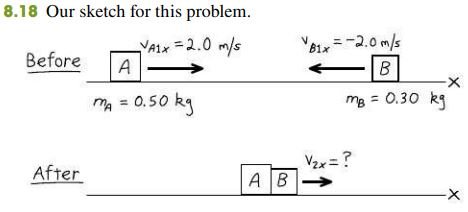
A COMPLETELY INELASTIC COLLISION
We repeat the collision described in Example 8.5 (Section 8.2), but this time equip the gliders so that they stick together when they collide. Find the common final x-velocity, and compare the initial and final kinetic energies of the system.
IDENTIFY and SET UP:
There are no external forces in the x-direction, so the x-component of momentum is conserved. Figure 8.18 shows our sketch. Our target variables are the final x-velocity, v_{2x}, and the initial and final kinetic energies, K_1 and K_1.
EXECUTE:
From conservation of momentum,
\begin{aligned}m_{A} v_{A 1 x}+m_{B} v_{B 1 x} &=\left(m_{A}+m_{B}\right) v_{2 x} \\v_{2 x} &=\frac{m_{A} v_{A 1x}+m_{B} v_{B 1 x}}{m_{A}+m_{B}} \\&=\frac{(0.50 \mathrm{~kg})(2.0 \mathrm{~m} / \mathrm{s})+(0.30\mathrm{~kg})(-2.0 \mathrm{~m} / \mathrm{s})}{0.50 \mathrm{~kg}+0.30 \mathrm{~kg}} \\&=0.50\mathrm{~m} / \mathrm{s}\end{aligned}Because v_{2x} is positive, the gliders move together to the right after the collision. Before the collision, the kinetic energies are
\begin{aligned}&K_{A}=\frac{1}{2} m_{A} v_{A 1 x}^{2}=\frac{1}{2}(0.50 \mathrm{~kg})(2.0\mathrm{~m}/ \mathrm{s})^{2}=1.0 \mathrm{~J} \\&K_{B}=\frac{1}{2} m_{B} v_{B 1 x}^{2}=\frac{1}{2}(0.30 \mathrm{~kg})(-2.0 \mathrm{~m} / \mathrm{s})^{2}=0.60 \mathrm{~J}\end{aligned}The total kinetic energy before the collision is K_{1}=K_{A}+K_{B} =1.6 J. The kinetic energy after the collision is
\begin{aligned}K_{2} &=\frac{1}{2}\left(m_{A}+m_{B}\right) v_{2 x}^{2}=\frac{1}{2}(0.50 \mathrm{~kg}+0.30 \mathrm{~kg})(0.50 \mathrm{~m} / \mathrm{s})^{2} \\&=0.10 \mathrm{~J}\end{aligned}
EVALUATE: The final kinetic energy is only \frac{1}{16} of the original; \frac{15}{16} is converted from mechanical energy to other forms. If there is a wad of chewing gum between the gliders, it squashes and becomes warmer. If there is a spring between the gliders that is compressed as they lock together, the energy is stored as potential energy of the spring. In both cases the total energy of the system is conserved, although kinetic energy is not. In an isolated system, however, momentum is always conserved whether the collision is elastic or not.
