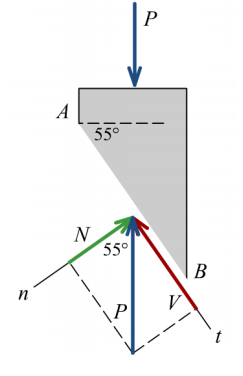
A compression load of P = 80 kips is applied to a 4 in. by 4 in. square post, as shown in Figure P1.38/39. Determine the normal stress perpendicular to plane AB and the shear stress parallel to plane AB.

Question

Accepted Answer

The angle θ for the inclined plane is 55°. The normal force N perpendicular to plane AB is found from

[latex]N=P \cos heta=(80 ext { kips }) \cos 55^{\circ}=45.8861 ext { kips }[/latex]

and the shear force V parallel to plane AB is

[latex]V=P \sin heta=(80 ext { kips }) \sin 55^{\circ}=65.5322 ext { kips }[/latex]

The cross-sectional area of the post is (4 in.)(4 in.) = 16 [latex] ext { in. }{ }^{2}[/latex], but the area along inclined plane AB is

[latex]A_{n}=A / \cos heta=\frac{16 in \cdot^{2}}{\cos 55^{\circ}}=27.8951 in .{ }^{2}[/latex]

The normal stress [latex]\sigma_{n}[/latex] perpendicular to plane AB is

[latex]\sigma_{n}=\frac{N}{A_{n}}=\frac{45.8861 kips }{27.8951 in .^{2}}=1.6449 ksi =1.645 ksi[/latex]

The shear stress [latex] au_{n t}[/latex] parallel to plane AB is

[latex] au_{n t}=\frac{V}{A_{n}}=\frac{65.5322 kips }{27.8951 in .^{2}}=2.3492 ksi =2.35 ksi[/latex]

Question 1.38: A compression load of P = 80 kips is applied to a 4 in. by 4...

Related Answered Questions