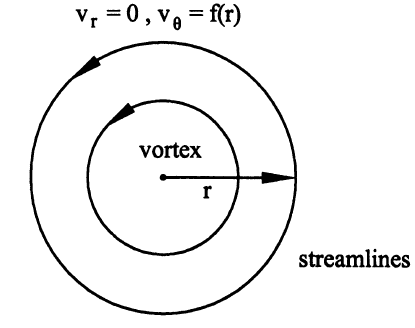
A forced vortex flow is given by v=rωoeθ, where ωo is constant (Fig. 8.16). Determine if Bernoulli’s equation can be used to determine the pressure differ-ence between two radial locations. Ignore gravity.

Question

A forced vortex flow is given by [latex] u =r\omega _{\omicron }\hat{e}_{ heta },[/latex] where [latex]\omega _{\omicron }[/latex] is constant (Fig. 8.16). Determine if Bernoulli’s equation can be used to determine the pressure differ-ence between two radial locations. Ignore gravity.

Accepted Answer

For [latex] u _{r}\hat{e}_{r}+ u _{ heta }\hat{e}_{ heta }+ u _{z}\hat{e}_{z},[/latex] we have

[latex] u _{r}=0, u _{ heta }=r\omega _{\omicron }, u _{z}=0.[/latex]

FIGURE 8.16 Schema of a vortex flow. In a forced vortex, [latex] u _{ heta }=r\omega ,[/latex] whereas in a free vortex, [latex] u _{ heta }=c/r,[/latex] where c is a constant. What is the vorticity for each?.

Fundamental Balance Relations To use the Bernoulli equation, several assumptions must be met:
1. The flow must be steady. Checking in each direction, we get

[latex] \frac{\partial}{\partial t}( u _{r})=0, \frac{\partial}{\partial t}(r\omega _{\omicron })=0, \frac{\partial}{\partial t}( u _{z})=0;[/latex]

thus, this restriction is satisfied.

2. The fluid must be incompressible. For cylindrical coordinates,

[latex] riangledown \cdot u =\frac{1}{r}\frac{\partial}{\partial r}(r u _{r})+\frac{1}{r}\frac{\partial}{\partial heta }( u _{ heta })+\frac{\partial}{\partial z}( u _{z}).[/latex]

Checking [latex] riangledown \cdot u =0,[/latex] we get

[latex] \frac{1}{r}\frac{\partial}{\partial r}(r(0))+\frac{1}{r}\frac{\partial}{\partial heta }( u \omega _{\omicron })+\frac{\partial}{\partial z}(0)=0;[/latex]

thus, this restriction is satisfied.

3. Under certain situations, we can assume that the fluid is inviscid. The validity of this assumption must be established via experience.
4. The flow must be along a streamline or it must be irrotational, where [latex] riangledown imes u =0.[/latex] For cylindrical coordinates, [latex] riangledown imes u =0[/latex] is given by

[latex]\left(\frac{1}{r}\frac{\partial u _{z}}{\partial heta }-\frac{\partial u _{ heta }}{\partial z} ight)\hat{e}_{r}+\left(\frac{\partial u _{r}}{\partial z}-\frac{\partial u _{z}}{\partial r} ight)\hat{e}_{ heta }+\left(\frac{1}{r}\frac{\partial (r u _{ heta })}{\partial r}-\frac{1}{r}\frac{\partial u _{r}}{\partial heta } ight)\hat{e}_{z}=0.[/latex]

With [latex] u _{r}= u _{z}=0,[/latex] we have

[latex] riangledown imes u =\left(-\frac{\partial u _{ heta }}{\partial z} ight)\hat{e}_{r}+\left(\frac{1}{r}\frac{\partial (r u _{ heta })}{\partial r} ight)\hat{e}_{z}=\frac{1}{r}\frac{\partial (r^{2}\omega _{\omicron })}{\partial r}\hat{e}_{z}[/latex]

or, in the z direction,

[latex] \frac{1}{r}(2r\omega _{\omicron })=2\omega _{0}.[/latex]

Therefore, the flow is not irrotational, and Bernoulli’s equation cannot be used unless along a streamline.

Question 8.9: A forced vortex flow is given by v=rωoeθ, where ωo is consta...

Related Answered Questions