A pipe with an outside diameter of 140 mm and a wall thickness of 7 mm is subjected to the 16-kN load shown in Figure P15.79. The internal pressure in the pipe is 2.50 MPa, and the yield strength of the steel is σY = 240 MPa. (a) Determine the factors of safety predicted at points H and K by the

Question

A pipe with an outside diameter of 140 mm and a wall thickness of 7 mm is subjected to the 16-kN load shown in Figure P15.79. The internal pressure in the pipe is 2.50 MPa, and the yield strength of the steel is [latex]\sigma_{Y}[/latex] = 240 MPa.
(a) Determine the factors of safety predicted at points H and K by the maximum-shear-stress theory of failure.
(b) Determine the Mises equivalent stresses at points H and K.
(c) Determine the factors of safety at points H and K predicted by the maximum-distortion-energy theory.

Accepted Answer

Section properties:

[latex]\begin{aligned}&d=140 mm -2(7 mm )=126 mm \&A=\frac{\pi}{4}\left[(140 mm )^{2}-(126 mm )^{2} ight]=2,924.823 mm ^{2} \&J=\frac{\pi}{32}\left[(140 mm )^{4}-(126 mm )^{4} ight]=12.970 imes 10^{6} mm ^{4} \&I_{y}=I_{z}=\frac{\pi}{64}\left[(140 mm )^{4}-(126 mm )^{4} ight]=6.485 imes 10^{6} mm ^{4} \&Q=\frac{1}{12}\left[(140 mm )^{3}-(126 mm )^{3} ight]=61,968.667 mm ^{3}\end{aligned}[/latex]

Vector expression for the 16-kN load:
The 16-kN load can be expressed in vector form as:

[latex]F =-(16 kN ) \sin 55^{\circ} j +(16 kN ) \cos 55^{\circ} k[/latex]

The equivalent forces acting at H and K are thus

[latex]\begin{aligned}&F_{x}=0 N \&F_{y}=-13,106.433 N \&F_{z}=9,177.223 N\end{aligned}[/latex]

The position vector from the section of interest to a point on the line of action of F is:

[latex]r =(0.7 m ) i +(1.3 m ) k[/latex]

The equivalent moments are found from the cross-product r × F.

[latex]\begin{aligned}r imes F &=\left|\begin{array}{ccc} i & j & k \0.7 & 0 & 1.3 \0 & -13,106.433 & 9,177.223\end{array} ight| \&=17,038.363 N - m i -6,424.056 N - m j -9,174.503 N - m k\end{aligned}[/latex]

Equivalent moments:

[latex]\begin{aligned}M_{x} &=17.0384 imes 10^{6} N - mm \M_{y} &=-6.4241 imes 10^{6} N - mm \M_{z} &=-9.1745 imes 10^{6} N - mm\end{aligned}[/latex]

Each of the non-zero forces and moments will be evaluated to determine whether stresses are created at the point of interest.

(a) Consider point H.
Force [latex]F_{y}[/latex] does not cause either a normal stress or a shear stress at H.

Force [latex]F_{z}[/latex] creates a transverse shear stress in the xz plane at H. The magnitude of this shear stress is:

[latex] au_{x z}=\frac{(9,177.223 N )\left(61,968.667 mm ^{3} ight)}{\left(6.485 imes 10^{6} mm ^{4} ight)[(140 mm )-(126 mm )]}=6.264 MPa[/latex]

Moment [latex]M _{x}[/latex], which is a torque, creates a torsion shear stress in the xz plane at H. The magnitude of this shear stress is:

[latex] au_{x z}=\frac{M_{x} c}{J}=\frac{\left(17.0384 imes 10^{6} N - mm ight)(140 mm / 2)}{12.970 imes 10^{6} mm ^{4}}=91.956 MPa[/latex]

Moment [latex]M _{y}[/latex] does not create bending stress at H because H is located on the neutral axis for bending about the y axis.

Moment [latex]M _{z}[/latex] creates bending stress at H. The magnitude of this stress is:

[latex]\sigma_{x}=\frac{M_{z} y}{I_{z}}=\frac{\left(9.1745 imes 10^{6} N - mm ight)(140 mm / 2)}{6.485 imes 10^{6} mm ^{4}}=99.031 MPa[/latex]

Stresses due to internal pressure:
The 2.50-MPa internal fluid pressure creates tension normal stresses in the 7-mm-thick wall of the pipe.
The longitudinal stress (which acts in the x direction) in the pipe wall is:

[latex]\sigma_{ ext {long }}=\frac{p d}{4 t}=\frac{(2.50 MPa )(126 mm )}{4(7 mm )}=11.25 MPa ( T )[/latex]

and the circumferential stress is:

[latex]\sigma_{ ext {hoop }}=\frac{p d}{2 t}=\frac{(2.50 MPa )(126 mm )}{2(7 mm )}=22.50 MPa ( T )[/latex]

The hoop stress acts in the z direction at H and in the y direction at K.

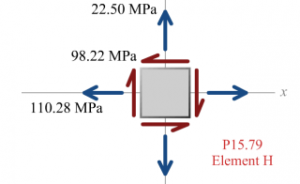
Summary of stresses at H:

[latex]\begin{aligned}\sigma_{x} &=99.030 MPa +11.25 MPa =110.280 MPa ( T ) \\sigma_{z} &=22.50 MPa ( T ) \ au_{x z} &=6.264 MPa +91.956 MPa =98.220 MPa\end{aligned}[/latex]

Principal stress calculations for point H:

[latex]\begin{aligned}\sigma_{p 1, p 2} &=\frac{(110.280 MPa )+(22.50 MPa )}{2} \pm \sqrt{\left(\frac{(110.280 MPa )-(22.50 MPa )}{2} ight)^{2}+(-98.220 MPa )^{2}} \&=66.390 MPa \pm 107.580 MPa\end{aligned}[/latex]

therefore, [latex]\sigma_{p 1}=173.970 MPa[/latex] and [latex]\sigma_{p 2}=-41.190 MPa[/latex]

Consider point K.
Force [latex]F _{y}[/latex] creates a transverse shear stress in the xy plane at K. The magnitude of this shear stress is:

[latex] au_{x y}=\frac{(13,106.433 N )\left(61,968.667 mm ^{3} ight)}{\left(6.485 imes 10^{6} mm ^{4} ight)[(140 mm )-(126 mm )]}=8.946 MPa[/latex]

Force [latex]F _{z}[/latex] does not cause either a normal stress or a shear stress at K.

Moment [latex]M _{x}[/latex], which is a torque, creates a torsion shear stress in the xy plane at K. The magnitude of this shear stress is:

[latex] au_{x y}=\frac{M_{x} c}{J}=\frac{\left(17.0384 imes 10^{6} N - mm ight)(140 mm / 2)}{12.970 imes 10^{6} mm ^{4}}=91.956 MPa[/latex]

Moment [latex]M _{y}[/latex] creates bending stress at K. The magnitude of this stress is:

[latex]\sigma_{x}=\frac{M_{y} z}{I_{y}}=\frac{\left(6.4241 imes 10^{6} N - mm ight)(140 mm / 2)}{6.485 imes 10^{6} mm ^{4}}=69.341 MPa[/latex]

Moment [latex]M _{z}[/latex] does not create bending stress at K because K is located on the neutral axis for bending about the z axis.

Summary of stresses at K:

[latex]\begin{aligned}\sigma_{x} &=-69.341 MPa +11.25 MPa =58.091 MPa ( C ) \\sigma_{y} &=22.50 MPa ( T ) \ au_{x y} &=-8.946 MPa -91.956 MPa =-100.902 MPa\end{aligned}[/latex]

Principal stress calculations for point K:

[latex]\begin{aligned}\sigma_{p 1, p 2} &=\frac{(-58.091 MPa )+(22.50 MPa )}{2} \pm \sqrt{\left(\frac{(-58.091 MPa )-(22.50 MPa )}{2} ight)^{2}+(-100.902 MPa )^{2}} \&=-17.796 MPa \pm 108.651 MPa\end{aligned}[/latex]

therefore, [latex]\sigma_{p 1}=90.855 MPa[/latex] and [latex]\sigma_{p 2}=-126.446 MPa[/latex]

(a) Maximum-Shear-Stress Theory
Element H:

[latex]\left|\sigma_{p 1}-\sigma_{p 2} ight|=|173.970 MPa -(-41.190 MPa )|=215.160 MPa[/latex]

The factor of safety associated with this state of stress is:

[latex]FS _{H}=\frac{240 MPa }{215.160 MPa }=1.115[/latex]

Element K:

[latex]\left|\sigma_{p 1}-\sigma_{p 2} ight|=|90.855 MPa -(-126.446 MPa )|=217.301 MPa[/latex]

The factor of safety associated with this state of stress is:

[latex]FS _{K}=\frac{240 MPa }{217.301 MPa }=1.104[/latex]

(b) Mises equivalent stresses at points H and K:
Element H:

[latex]\begin{aligned}\sigma_{M, H} &=\left[\sigma_{p 1}^{2}-\sigma_{p 1} \sigma_{p 2}+\sigma_{p 2}^{2} ight]^{1 / 2} \&=\left[(173.970 MPa )^{2}-(173.970 MPa )(-41.190 MPa )+(-41.190 MPa )^{2} ight]^{1 / 2} \&=197.809 MPa =197.8 MPa\end{aligned}[/latex]

Element K:

[latex]\begin{aligned}\sigma_{M, K} &=\left[\sigma_{p 1}^{2}-\sigma_{p 1} \sigma_{p 2}+\sigma_{p 2}^{2} ight]^{1 / 2} \&=\left[(90.855 MPa )^{2}-(90.855 MPa )(-126.446 MPa )+(-126.446 MPa )^{2} ight]^{1 / 2} \&=189.028 MPa =189.0 MPa\end{aligned}[/latex]

(c) Maximum-Distortion-Energy Theory:
Element H:

[latex]FS _{H}=\frac{240 MPa }{197.809 MPa }=1.213[/latex]

Element K:

[latex]FS _{K}=\frac{240 MPa }{189.028 MPa }=1.270[/latex]

Question 15.79: A pipe with an outside diameter of 140 mm and a wall thickne...

Related Answered Questions