Question 2.9: A section of a piping system is acted on by the three couple...

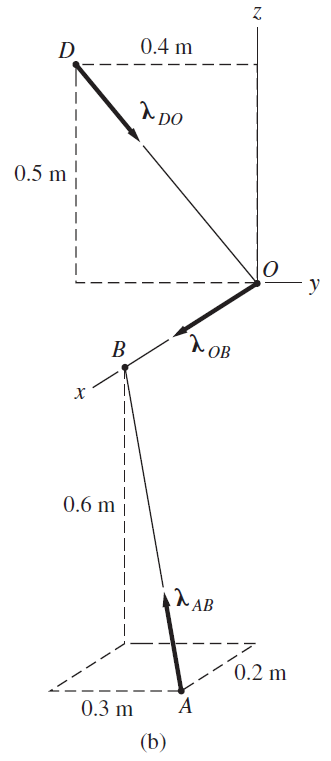
Applying the right-hand rule to each of the three couples in Fig. (a), we see that the corresponding couple-vectors will be directed as follows: C_{1}, from point D toward point O; C_{2}, from point O toward point B; and C_{3}, from point A toward point B. Because these couple-vectors do not have the same directions, the most practical method of determining their resultant is to use the vector equation

Using the three unit vectors shown in Fig. (b), the couple-vectors C_{1}, C_{2}, and C_{3} can be written as

Adding these three couple-vectors gives

The magnitude of C_{R} is

and the direction cosines of C^{R} are the components of the unit vector λ directed along C^{R}:

\lambda _{x }=\frac{50}{99.41}=0.503        \lambda _{y}=-\frac{28.76}{99.41}=−0.289        \lambda _{z}=\frac{80.96}{99.41}=0.814

The resultant couple-vector is shown in Fig. (c). Although C^{R} is shown at point O, it must be remembered that couples are free vectors, so that C^{R} could be shown acting anywhere.The couple-vector C^{R} can be represented as two equal and opposite parallel forces. However, because the two forces will lie in a plane perpendicular to the couple-vector, in this case a skewed plane, this representation is inconvenient here.In general, given two forces that form a couple, the corresponding couplevector is easily determined (e.g., by summing the moments of the two forces about any point). However, given a couple-vector, it is not always convenient (or even desirable) to determine two equivalent forces.