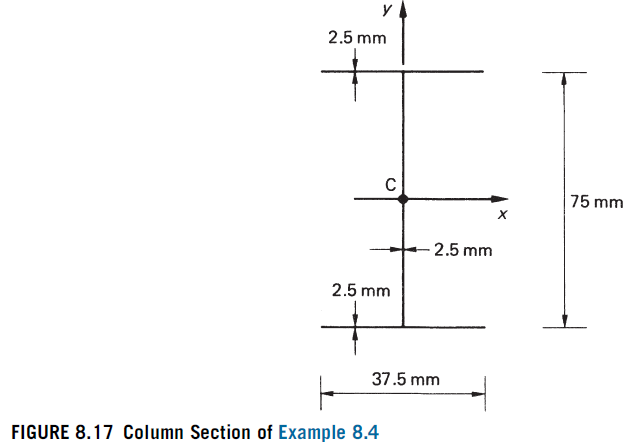
A thin-walled pin-ended column is 2 m long and has the cross-section shown in Fig. 8.17. If the ends of the column re free to warp, determine the lowest value of axial load which causes buckling and specify the buckling mode. Take E=75,000 N / mm ^{2} and G=21,000 N / mm ^{2}.
Question 8.4: A thin-walled pin-ended column is 2 m long and has the cross...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
Since the cross-section of the column is doubly symmetrical, the shear center coincides with the centroid of area and x_{S}=y_{S}=0; Eqs. (8.74), (8.75), and (8.76) therefore apply. Further, the boundary conditions are those of the column whose buckled shape is defined by Eqs. (8.71), so that the buckling load of the column is the lowest of the three values given by Eqs. (8.77).
E I_{x x} \frac{ d ^{2} v}{ d z^{2}}=-P v (8.74)
E I_{y y} \frac{ d ^{2} u}{ d z^{2}}=-P u (8.75)
E \Gamma \frac{ d ^{4} \theta}{ d z^{4}}-\left(G J-I_{0} \frac{P}{A}\right) \frac{ d ^{2} \theta}{ d z^{2}}=0 (8.76)
u=A_{1} \sin \frac{\pi z}{L}, \quad v=A_{2} \sin \frac{\pi z }{L} \quad \theta=A_{3} \sin \frac{\pi z}{L} (8.71)
P_{ CR (x x)}=\frac{\pi^{2} E I_{x x}}{L^{2}} P_{ CR (y y)}=\frac{\pi^{2} E I_{y y}}{L^{2}} P_{ CR (\theta)}=\frac{A}{I_{0}}\left(G J+\frac{\pi^{2} E \Gamma}{L^{2}}\right) (8.77)
The cross-sectional area A of the column is
A=2.5(2 \times 37.5+75)=375 mm ^{2}
The second moments of area of the cross-section about the centroidal axes Cxy are (see Chapter 15), respectively,
I_{x x}=2 \times 37.5 \times 2.5 \times 37.5^{2}+2.5 \times 75^{3} / 12=3.52 \times 10^{5} mm ^{4}
I_{y y}=2 \times 2.5 \times 37.5^{3} / 12=0.22 \times 10^{5} mm ^{4}
The polar second moment of area I_{0} is
I_{0}=I_{x x}+I_{y y}+A\left(x_{ S }^{2}+y_{ S }^{2}\right) \quad \text { (see the derivation of Eq. (8.69)) }
T(z)=P\left(x_{ S } \frac{ d ^{2} v}{ d z^{2}}-y_{ S } \frac{ d ^{2} u}{ d z^{2}}\right)-I_{0} \frac{P}{A} \frac{ d ^{2} \theta}{ d z^{2}} (8.69)
that is
I_{0}=3.52 \times 10^{5}+0.22 \times 10^{5}=3.74 \times 10^{5} mm ^{4}
The torsion constant J is obtained using Eq. (17.11), which gives
J=\sum \frac{s t^{3}}{3} \quad \text { or } \quad J=\frac{1}{3} \int_{\text {sect }} t^{3} d s (17.11)
J=2 \times 37.5 \times 2.5^{3} / 3+75 \times 2.5^{3} / 3=781.3 mm ^{4}
Finally, \Gamma is found using the method of Section 27.2 of Ref. 3 and is
\Gamma=2.5 \times 37.5^{3} \times 75^{2} / 24=30.9 \times 10^{6} mm ^{6}
Substituting these values in Eqs. (8.77), we obtain
P_{ CR (x x)}=6.5 \times 10^{4} N , \quad P_{ CR (y y)}=0.41 \times 10^{4} N , \quad P_{ CR (\theta)}=2.22 \times 10^{4} N
The column therefore buckles in bending about the Cy axis when subjected to an axial load of 0.41 \times 10^{4} N.
Related Answered Questions
The torsion bending constant \Gamma...
In this case, the shear center S is positioned on ...
The bending moment at any section of the column is...
The column is shown in its displaced position in F...