Question 9.30: A transmission shaft supported between two bearings and carr...

\text { Given } E=207000 N / mm ^{2} d=50 mm .

m_{A}=35 kg \quad m_{B}=55 kg .

Step I Deflections at mass-A and mass-B
Suppose the masses of 35 and 55 kg are attached to the shaft at points A and B respectively.

W_{A}=35 g =35(9.81)=343.35 N .

W_{B}=55 g =55(9.81)=539.55 N .

The deflections at these masses are calculated by the method of superimposition. The configuration is similar to Case 7 of Table 9.4 (simply supported beam with intermediate load). Rewriting Eqs (27) and (28) with reference to Fig. 9.55(a),

Table 9.4 Bending moment and deflection of beams

	Case 1 Cantilever Beam – End load (A) Bending moments \left(M_{b}\right) \text { at } O=-P l.         (1). \left(M_{b}\right) \text { at } x=-P(l-x) .             (2). (B) Deflections \delta \text { at } x=\frac{P x^{2}}{6 E I}(x-3 l)              (3). \delta_{\max .} \text { at }(x=l)=-\frac{P l^{3}}{3 E I}              (4).
	Case 2 Cantilever Beam—Uniformly distributed load (A) Bending moments \left(M_{b}\right) \text { at } O=-\frac{w l^{2}}{2}            (5). \left(M_{b}\right) \text { at } x=-\frac{w(l-x)^{2}}{2}             (6). (B) Deflections \delta \text { at } x=\frac{w x^{2}}{24 E I}\left(4 l x-x^{2}-6 l^{2}\right)            (7). \delta_{\max .} \text { at }(x=l)=-\frac{w l^{4}}{8 E I}           (8).
	Case 3 Cantilever Beam—Moment load (A) Bending moments \left(M_{b}\right) \text { at } O=\left(M_{b}\right) \text { at } x=\left(M_{b}\right)_{B}            (9). (B) Deflections \delta \text { at } x=\frac{\left(M_{b}\right)_{B} x^{2}}{2 E I}           (10). \delta_{\max .} \text { at }(x=l)=\frac{\left(M_{b}\right)_{B} l^{2}}{2 E I}          (11).
	Case 4 Simply supported beam—Centre load (A) Bending moments \left(M_{b}\right) \text { at } x=\frac{P x}{2}            (12). \left(M_{b}\right) \text { at } x=\frac{P(l-x)}{2} \quad(x>1 / 2)            (13). \left(M_{b}\right) \text { at } B=\frac{P l}{4}          (14). (B) Deflections \delta \text { at } x=\frac{P x\left(4 x^{2}-3 l^{2}\right)}{48 E I} \quad(0<x<1 / 2)              (15). \delta_{\max .} \text { at } B=-\frac{P l^{3}}{48 E I}                   (16).
	Case 5 Simply supported Beam—Uniformly distributed load (A) Bending moments \left(M_{b}\right) \text { at } x=\frac{w x(l-x)}{2}         (17). \left(M_{b}\right) \text { at } l / 2=\frac{w l^{2}}{8}           (18). (B) Deflections \delta \text { at } x=\frac{w x\left(2 l x^{2}-x^{3}-l^{3}\right)}{24 E I}            (19), \delta_{\max .} \text { at } l / 2=-\frac{5 w l^{4}}{384 E I}                 (20).
	Case 6 Simply supported beam—Moment load (A) Bending moments \left(M_{b}\right) \text { at } x=\frac{\left(M_{b}\right)_{B} x}{l}(0<x<a)                     (21). \left(M_{b}\right) \text { at } x=\frac{\left(M_{b}\right)_{B}(x-l)}{l}(a<x<l)               (22). (B) Deflections \delta \text { at } x=\frac{\left(M_{b}\right)_{B} x\left(x^{2}+3 a^{2}-6 a l+2 l^{2}\right)}{6 E I l} \quad(0<x< a )           (23). \delta \text { at } x=\frac{\left(M_{b}\right)_{B}\left[x^{3}-3 l x^{2}+x\left(2 l^{2}+3 a^{2}\right)-3 a^{2} l\right]}{6 E I l}           (a < x < l)              (24).
	Case 7 Simply supported Beam—Intermediate load (A) Bending moment \left(M_{b}\right) \text { at } x=\frac{P b x}{l} \quad(0<x<a)             (25). \left(M_{b}\right) \text { at } x=\frac{P a(l-x)}{l} \quad( a <x<l)           (26). (B) Deflections \delta \text { at } x=\frac{P b x\left(x^{2}+b^{2}-l^{2}\right)}{6 E I l} \quad(0<x<a)        (27). \delta \text { at } x=\frac{P a(l-x)\left(x^{2}+a^{2}-2 l x\right)}{6 E I l}(a<x<l)            (28).
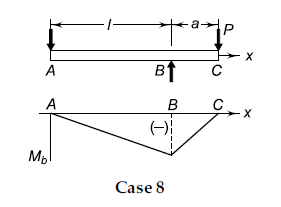	Case 8 Simply supported beam—Overhang load (A) Bending moments \left(M_{b}\right) \text { at } x=-\frac{P a x}{l} \quad(x<l) .             (29) \left(M_{b}\right) \text { at } x=P(x-l-a) \quad(x>l)           (30) (B) Deflections \delta \text { at } x=\frac{\operatorname{Pax}\left(l^{2}-x^{2}\right)}{6 E I l} \quad(x<l)          (31). \delta \text { at } x=\frac{P(x-l)\left[(x-l)^{2}-a(3 x-l)\right]}{6 E I} \quad(x>l)            (32). \delta \text { at } C=-\frac{P a^{2}(l+a)}{3 E I}             (33).

\tau=\frac{2 M_{t}}{d b l}                 (9.27).

\sigma_{c}=\frac{4 M_{t}}{d h l}            (9.28)

\delta \text { at } x=\frac{P b x\left(x^{2}+b^{2}-l^{2}\right)}{6 E I l} \quad(0<x<a)             (a).

\delta \text { at } x=\frac{P a(l-x)\left(x^{2}+a^{2}-2 l x\right)}{6 E I l}(a<x<l)               (b).

Deflections due to force 343.35 N [Fig. 9.55 (b)]
a = 750 mm b = 1500 mm l = 2250 mm
The deflection \left(\delta_{A}\right)_{A} at the point A due to the force at A is given by Eq. (a).

x=750 mm (0<x<a) .

\left(\delta_{A}\right)_{A}=\frac{\operatorname{Pbx}\left(x^{2}+b^{2}-l^{2}\right)}{6 E I l} .

\left(\delta_{A}\right)_{A}=\frac{(343.55)(1500)(750)\left(750^{2}+1500^{2}-2250^{2}\right)}{6 E I(2250)} .

=\frac{-6.44(10)^{10}}{E I}              (i).

The deflection \left(\delta_{B}\right)_{A} at the point B due to the
force at A is given by Eq. (b).

x = 1750 mm              (x > a).

\left(\delta_{B}\right)_{A}=\frac{P a(l-x)\left(x^{2}+a^{2}-2 l x\right)}{6 E I l} .

\left(\delta_{B}\right)_{A}=\frac{(343.35)(750)(2250-1750)\left[1750^{2}+750^{2}-2(2250)(1750)\right]}{6 E I(2250)} .

=\frac{-4.05(10)^{10}}{E I}                   (ii).

Deflections due to force 539.55 N            [Fig. 9.55(c)]
a = 1750 mm            b = 500 mm             l = 2250 mm.

The deflection \left(\delta_{A}\right)_{B} at the point A due to the
force at B is given by Eq. (a).
x = 750 mm              (0 < x < a).

\left(\delta_{A}\right)_{B}=\frac{P b x\left(x^{2}+b^{2}-l^{2}\right)}{6 E I l} .

\left(\delta_{A}\right)_{B}=\frac{(539.55)(500)(750)\left(750^{2}+500^{2}-2250^{2}\right)}{6 E I(2250)} .

=\frac{-6.37(10)^{10}}{E I}                 (iii).

The deflection \left(\delta_{B}\right)_{B} at the point B due to the
force at B is given by Eq. (a).

x =1 750 mm              (0 < x < a).

\left(\delta_{B}\right)_{B}=\frac{P b x\left(x^{2}+b^{2}-l^{2}\right)}{6 E I l} .

\left(\delta_{B}\right)_{B}=\frac{(539.55)(500)(1750)\left(1750^{2}+500^{2}-2250^{2}\right)}{6 E I(2250)} .

=\frac{-6.12(10)^{10}}{E I}             (iv).

Superimposing the deflections,

\delta_{A}=\left(\delta_{A}\right)_{A}+\left(\delta_{A}\right)_{B} .

=\frac{-6.44(10)^{10}}{E I}+\frac{-6.37(10)^{10}}{E I}=\frac{-12.81(10)^{10}}{E I} .

\delta_{B}=\left(\delta_{B}\right)_{A}+\left(\delta_{B}\right)_{B} .

=\frac{-4.05(10)^{10}}{E I}+\frac{-6.12(10)^{10}}{E I}=\frac{-10.17(10)^{10}}{E I} .

The negative sign indicates downward deflection and it is neglected.

I=\frac{\pi d^{4}}{64}=\frac{\pi(50)^{4}}{64} mm ^{4} .

Substituting values of I and E,

\delta_{A}=\frac{-12.81(10)^{10}}{E I}=\frac{-12.81(10)^{10}}{(207000)\left(\frac{\pi(50)^{4}}{64}\right)} .

=2.017 mm =2.017\left(10^{-3}\right) m .

\delta_{B}=\frac{-10.17(10)^{10}}{E I}=\frac{-10.17(10)^{10}}{(207000)\left(\frac{\pi(50)^{4}}{64}\right)} .

=1.601 mm =1.601\left(10^{-3}\right) m .

Step II Critical speed of shaft
From Eq. (9.57),

\omega_{n}=\sqrt{\frac{g\left(W_{1} \delta_{1}+W_{2} \delta_{2}+\ldots \ldots . .\right)}{\left(W_{1} \delta_{1}^{2}+W_{2} \delta_{2}^{2}+\ldots \ldots . .\right)}}                    (9.57).

\omega_{n}=\sqrt{\frac{g\left(W_{1} \delta_{1}+W_{2} \delta_{2}\right)}{\left(W_{1} \delta_{1}^{2}+W_{2} \delta_{2}^{2}\right)}} .

=\sqrt{\frac{(9.81)\left[(343.35)(2.017)\left(10^{-3}\right)+(539.55)(1.601)\left(10^{-3}\right)\right]}{\left[(343.35)(2.017)^{2}\left(10^{-3}\right)^{2}+(539.55)(1.601)^{2}\left(10^{-3}\right)^{2}\right]}} .

=\sqrt{\frac{9.81(1556.36)(10)^{-3}}{2779.82(10)^{-6}}} .

= 74.11 rad/s
(1 revolution = 2p radians).

=\frac{74.11(60)}{2 \pi}=707.7 rpm .