Adiabatic Flame Temperature Calculation
An equimolar gaseous mixture of benzene and ethylene at 300 K is fed into a reactor, where ethyl benzene is formed. If the reactor is operated adiabatically at a pressure of 1 bar, and the reactor effluent is in chemical equilibrium, find the reactor effluent temperature and species concentrations.
Data: See Appendices A.II and A.IV.
Since the reactor effluent is in equilibrium, we can write
K_{a}\left(T_{a d}\right)=\frac{a_{ EB }}{a_{ E } a_{ B }}=\frac{y_{ EB }\left(\frac{P}{1 bar }\right)}{y_{ E }\left(\frac{P}{1 bar }\right) y_{ B }\left(\frac{P}{1 bar }\right)}=\frac{y_{ EB }}{y_{ E } y_{ B }}
where we have assumed ideal gas mixture behavior and used the fact that the pressure in the reactor is 1 bar.Using the following table, the three mole fractions in this equation can be replaced by the single molar extent-of-reaction variable X.
| Inlet | Outlet | Outlet Mole Fraction | |
| C _{6} H _{6} | 1 | 1 − X | (1 − X)/(2 − X) |
| C _{2} H _{4} | 1 | 1 − X | (1 − X)/(2 − X) |
| C _{6} H _{5} C _{2} H _{5} | 0 | X | X/(2 − X) |
| 2 − X | |||
Thus, we have
K_{a}\left(T_{a d}\right)=\frac{X(2-X)}{(1-X)^{2}}
so that
X=1-\sqrt{\frac{1}{1+K\left(T_{a d}\right)}}
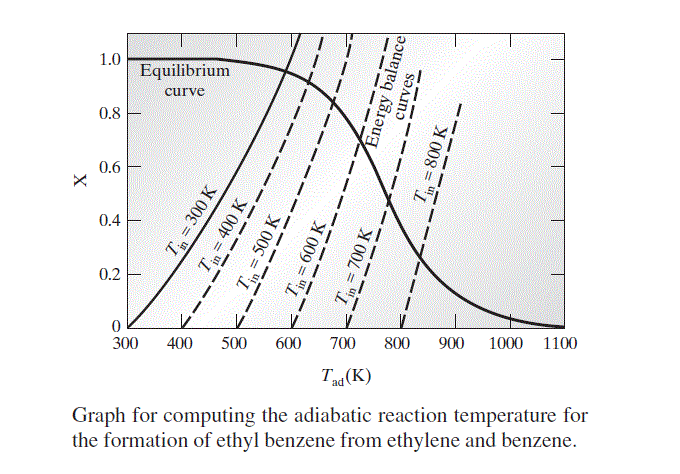
With the data given in Appendix A, and Eq. 13.1-23b, it is possible to compute the value of K_{a} at any temperature. Once K_{a} is known, X can be computed. The equilibrium values of X calculated in this manner for various values of T_{a d} are plotted in the following figure.
K_{x}=\prod_{ i } x_{ i }^{\nu_{ i }} \quad \text { and } \quad K_{y}=\prod_{ i } y_{ i }^{\nu_{ i }} (13.1-23b)
The adiabatic reaction temperature also must satisfy the energy balance equation; using Eq. 14.3-10a, we have
0=\sum_{ i =1}^{ C }\left(N_{ i }\right)_{\text {in }} \int_{T_{ in }}^{T_{a d}} C_{ P , i } d T+\sum_{ j =1}^{ M }\left[\Delta_{ rxn , j } H\left(T_{a d}\right)\right] X_{ j } (14.3-10a)
0=\int_{T_{ in }}^{T_{a d}}\left(C_{ P , B }+C_{ P , E }\right) d T+\Delta_{ rxn } H\left(T_{a d}\right) X
or
X=\frac{-\int_{T_{ in }}^{T_{a d}}\left(C_{ P , B }+C_{ P , E }\right) d T}{\Delta_{ rxn } H\left(T_{a d}\right)}
where the heat capacity data for benzene and ethylene are given in Appendix A.II. Using this equation, the molar extent of reaction needed to satisfy the energy balance for fixed values of T_{\text {in }} and Tad can be computed. Since the inlet temperature is fixed at 300 K, we will use this equation to compute values of the molar extent of reaction X for a number of different choices of T_{a d}; the results of this calculation are plotted in the figure. For illustration, energy balance X-T_{a d} curves for several other values of the reactor inlet temperature are given as dashed lines.
The adiabatic reaction temperature and the equilibrium extent of reaction X that satisfy both the equilibrium and the energy balance relations for a given value of T_{\text {in }} are found at the intersection of the equilibrium and energy balance curves in the figure. For the reactor feed at 300 K this occurs at
\begin{aligned}T_{a d} & \simeq 588 K \\X & \simeq 0.955\end{aligned}
Thus
\begin{aligned}y_{ B }=y_{ E } &=0.045 / 1.045=0.043 \\y_{ EB } &=0.955 / 1.045=0.914\end{aligned}
The results for other reactor feed temperatures Tin can be computed in a similar fashion from the data in the figure.
Using Aspen Plus^R and the folder Aspen Illustration>Chapter 14>14.3-2 on the Wiley website for this book that uses both the REquil and RGibbs reactor blocks, which led to the same answers, the following results were obtained:
\begin{aligned}T &=640.8 K \\y_{ B }=y_{ E } &=0.0949 \\y_{ EB } &=0.8102\end{aligned}
These results are not in good agreement with the results above for this illustration.]
