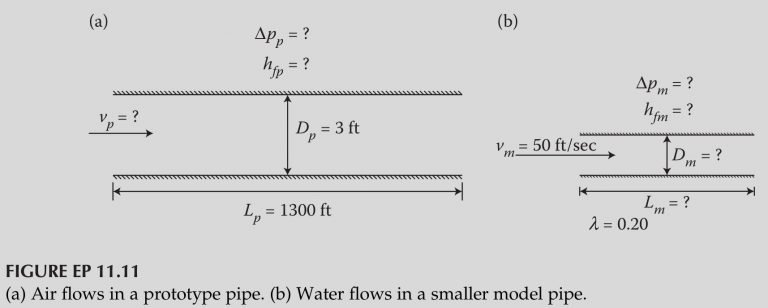
Air at 68^{ \circ} F flows in a prototype 1300-ft-long circular pipe with a diameter of 3 ft and an absolute pipe roughness of 0.03 ft, as illustrated in Figure EP 11.11. A smaller model of the larger prototype is designed in order to study the flow characteristics of turbulent pipe flow. The model fluid is water at 70^{ \circ} F , the velocity of water in the smaller model pipe is 50 ft/sec, and the model scale, λ is 0.2. The flow resistance is modeled by the friction factor, f = 8 C_{D} . (a) Determine the pressure drop (and head loss) in the flow of the water in the model. (b) Determine the velocity flow of the air in the prototype pipe flow in order to achieve dynamic similarity between the model and the prototype. (c) Determine the pressure drop (and head loss) in the flow of the air in the prototype in order to achieve dynamic similarity between the model and the prototype.
Question 11.11: Air at 68^◦ F flows in a prototype 1300-ft-long circular pip...
Learn more on how we answer questions.
(a) In order to determine the pressure drop (and head loss) in flow of the water in the model, the major head loss equation, Equation 11.122 h_{f} = \frac{\tau _{w}L}{\gamma R_{h}} = \frac{\Delta p}{\gamma } = S_{f}L = C_{D}\rho v^{2} \frac{L}{\gamma R_{h}} = \frac{v^{2}L}{C^{2}R_{h}} = f \frac{L}{D} \frac{v^{2}}{2g} = \left(\frac{vn}{R_{h}^{2/3}} \right)^{2}L , is applied as follows:
h_{f} = \frac{\Delta p}{\gamma } = f \frac{L}{D} \frac{v^{2}}{2g}where the friction factor, f is used to model the flow resistance. Because the Reynolds number, R > 4,000 (turbulent pipe flow) is assumed, the friction factor, f is only a function of ɛ/D and independent of R, as illustrated in by the Moody diagram in Figure 8.1. However the Colebrook equation, Equation 8.33 C = \sqrt{\frac{8g}{f} } , presents a mathematical representation of the Moody diagram in Figure 8.1. Furthermore, in order to determine the length, diameter, and the absolute pipe roughness of the model pipe, the model scale, λ (inverse of the length ratio) is applied. The fluid properties for water are given in Table A.2 in Appendix A.
D_{p}: = 3 ft L_{p}: = 1300 ft \varepsilon _{p} : = 0.03 ft \lambda : = 0.2
Guess value: D_{m}: = 0.1 ft L_{m}: = 1 ft \varepsilon _{m}: = 0.01 ft
Given
\lambda = \frac{D_{m}}{D_{p}} \lambda = \frac{L_{m}}{L_{p}} \lambda = \frac{\varepsilon _{m}}{\varepsilon _{p}}
\left ( \begin{matrix} D_{m} \\ L_{m} \\ \varepsilon _{m} \end{matrix} \right ) : = Find (D_{m}, L_{m}, \varepsilon _{m}) = \left ( \begin{matrix} 0.6 \\ 260 \\ 6 \times 10^{-3} \end{matrix} \right ) ft
slug: = 1 lb \frac{sec^{2}}{ft} \rho _{m} : = 1.936 \frac{slug}{ft^{3}} \mu _{m} : = 20.5 \times 10^{-6} lb \frac{sec}{ft^{2}}
g: = 32.174 \frac{ft}{sec^{2}} \gamma _{m}: = \rho _{m}. g = 62.289 \frac{lb}{ft^{3}} V_{m}: = 50 \frac{ft}{sec}
R_{m}: = \frac{\rho _{m} .V_{m} .D_{m}}{\mu _{m}} = 2.833 \times 10^{6}Guess value: h_{fm}: = 1 ft \Delta P_{m}: = 1 \frac{lb}{ft^{2}} f_{m}: = 0.01
Given
h_{fm} = f_{m} \frac{L_{m}}{D_{m}} \frac{v^{2}_{m}}{2g} \frac{1}{\sqrt{f_{m}} } = – 2 log \left(\frac{\frac{\varepsilon _{m}}{D_{m}} }{3.7} + \frac{2.51 }{R_{m}. \sqrt{f_{m}} } \right)
\Delta P_{m} = h_{fm} . \gamma _{m}
\left ( \begin{matrix} h_{fm} \\ \Delta P_{m} \\ f_{m} \end{matrix} \right ) : = Find (h_{fm, \Delta P_{m} , f_{m}})
h_{fm}= 638.493 ft \Delta P_{m} = 3.977 \times 10^{4} \frac{lb}{ft^{2}} f_{m}= 0.038
(b)–(c) To determine the velocity flow of the air in the prototype pipe flow in order to achieve dynamic similarity between the model and the prototype for turbulent pipe flow and to determine the pressure drop (and head loss) in the flow of the air in the prototype in order to achieve dynamic similarity between the model and the prototype for turbulent pipe flow, the ɛ/D must remain a constant between the model and prototype as follows:
\left(\frac{\varepsilon}{D} \right)_{p} = \left(\frac{\varepsilon }{D } \right)_{m}
\frac{\varepsilon _{p}}{D_{p}} = 0.01 \frac{\varepsilon _{m}}{D_{m}} = 0.01
However, because the friction factor, f is in dependent of R for turbulent flow, R does not need to remain a constant between the model and the prototype.
(b)–(c) To determine the velocity flow of the air in the prototype pipe flow in order to achieve dynamic similarity between the model and the prototype for turbulent pipe flow and to determine the pressure drop (and head loss) in the flow of the air in the prototype in order to achieve dynamic similarity between the model and the prototype for turbulent pipe flow, the friction factor, f must remain a constant between the model and the prototype (which is a direct result of maintaining a constant ɛ/D between the model and the prototype, and applying the “pressure model” similitude scale ratio, specifically the velocity ratio, v r given in Table 11.1) as follows:
\underbrace{\left[\frac{\frac{h_{f}}{v^{2}L} }{2gD} \right]_{p} }_{f_{p}} = \underbrace{\left[\frac{\frac{h_{f}}{v^{2}L} }{2gD} \right]_{m} }_{f_{m}}
v_{r} = \frac{v_{p}}{v_{m}} = \frac{\left(\sqrt{\frac{\Delta p}{\rho } } \right)_{p} }{\left(\sqrt{\frac{\Delta p}{\rho } } \right)_{m} } = \Delta p_{r}^{\frac{1}{2} } \rho _{r}^{\frac{-1}{2} }
The fluid properties for air are given in Table A.5 in Appendix A.
\rho _{p} : = 0.00231 \frac{slug}{ft^{3}} \mu _{p} : = 0.376 \times 10^{-6} lb \frac{sec}{ft^{2}} \gamma _{p} : = \rho _{p}. g = 0.074 \frac{lb}{ft^{3}}
Guess value: V_{p}: = 1 \frac{ft}{sec} h_{fp}: = 1 ft \Delta p_{p}: = 1 \frac{lb}{ft^{2}} f_{p}: = 0.01
Given
f_{p} = \frac{h_{fp}}{\left(\frac{V^{2}_{p}. L_{p}}{2.g. D_{p}} \right) } \frac{V_{P}}{\Delta p_{p}^{\frac{1}{2} }. \rho _{p}^{\frac{- 1}{2}} } = \frac{V_{m}}{\Delta p_{m}^{\frac{1}{2} }. \rho _{m}^{\frac{- 1}{2}} }
f_{p} = f_{m} \Delta p_{p} = h_{fp}. \gamma _{p}
\left ( \begin{matrix} V_{p} \\ h_{fp} \\ \Delta p_{p} \\ f_{p} \end{matrix} \right ) : = Find ( V_{p}, h_{fp},\Delta p_{p}, f_{p})
V_{p} = 7.857 \frac{ft}{s} h_{fp} = 15.766 ft \Delta p_{p} = 1.172 \frac{lb}{ft^{2}} f_{p}: = 0.038
Furthermore, the Euler number, E remains a constant between the model and the prototype as follows:
E_{m}: = \frac{\rho _{m}. V^{2}_{m}}{\Delta p_{m}} = 0.122 E_{p}: = \frac{\rho _{p}. V^{2}_{p}}{\Delta p_{p}} = 0.122
Therefore, although the similarity requirements regarding the independent π term, \varepsilon /D ((\varepsilon /D)_{p} = (\varepsilon /D)_{m} = 0.01) and the dependent π term, E (“pressure model”) ( E_{p} = E_{m} = 0.122) are theoretically satisfied, the dependent π term (i.e., the friction factor, f ) will actually/practically remain a constant between the model and its prototype ( f_{p} = f_{m} = 0.038) only if it is practical to attain/maintain the model velocity, pressure, fluid, scale, and cost. Furthermore, because the friction factor, f is independent of R for turbulent flow, R does not need to remain a constant between the model and the prototype as follows:
R_{m} = 2.833 \times 10^{6} R_{p} : = \frac{\rho _{p} . V_{p}. D_{p}}{\mu _{p}} = 1.1448 \times 10^{5}
| Table A.2 | |||||||
| Physical Properties for Water at Standard Sea-Level Atmospheric Pressure as a Function of Temperature | |||||||
| Temperature (θ) ^{\circ } F |
Density (ρ) slug/ft^{3} |
Specific Weight (γ) Ib/ft^{3} |
Absolute (Dynamic) Viscosity (μ) 10^{-6} Ib-sec/ft^{3} |
Kinematic Viscosity (ν) 10^{-6} ft^{2}/sec |
Surface Tension (σ) lb=ft |
Vapor Pressure (\rho _{\nu } ) psia |
Bulk Modulus of Elasticity (E_{\upsilon } ) psi |
| 32 | 1.940 | 62.42 | 37.46 | 19.31 | 0.00518 | 0.0885 | 293,000 |
| 40 | 1.940 | 62.43 | 32.29 | 16.64 | 0.00514 | 0.1220 | 294,000 |
| 50 | 1.940 | 62.41 | 27.35 | 14.10 | 0.00509 | 0.1780 | 305,000 |
| 60 | 1.938 | 62.37 | 23.59 | 12.17 | 0.00504 | 0.2560 | 311,000 |
| 70 | 1.936 | 62.30 | 20.50 | 10.59 | 0.00498 | 0.3630 | 320,000 |
| 80 | 1.934 | 62.22 | 17.99 | 9.30 | 0.00492 | 0.5070 | 322,000 |
| 90 | 1.931 | 62.11 | 15.95 | 8.26 | 0.00486 | 0.6980 | 323,000 |
| 100 | 1.927 | 62.00 | 14.24 | 7.39 | 0.00480 | 0.9490 | 327,000 |
| 110 | 1.923 | 61.86 | 12.84 | 6.67 | 0.00473 | 1.2750 | 331,000 |
| 120 | 1.918 | 61.71 | 11.68 | 6.09 | 0.00467 | 1.6920 | 333,000 |
| 130 | 1.913 | 61.55 | 10.69 | 5.58 | 0.00460 | 2.2200 | 334,000 |
| 140 | 1.908 | 61.38 | 9.81 | 5.14 | 0.00454 | 2.8900 | 330,000 |
| 150 | 1.902 | 61.20 | 9.05 | 4.76 | 0.00447 | 3.7200 | 328,000 |
| 160 | 1.896 | 61.00 | 8.38 | 4.42 | 0.00441 | 4.7400 | 326,000 |
| 170 | 1.890 | 60.80 | 7.80 | 4.13 | 0.00434 | 5.9900 | 322,000 |
| 180 | 1.883 | 60.58 | 7.26 | 3.85 | 0.00427 | 7.5100 | 318,000 |
| 190 | 1.876 | 60.36 | 6.78 | 3.62 | 0.00420 | 9.3400 | 313,000 |
| 200 | 1.868 | 60.12 | 6.37 | 3.41 | 0.00413 | 11.5200 | 308,000 |
| 212 | 1.860 | 59.83 | 5.93 | 3.19 | 0.00404 | 14.6900 | 300,000 |
| ^{\circ } C | kg/m^{3} | KN/m^{3} | N-sec/m^{2} | 10^{-6} m^{2} /sec | N/m | KN/m^{2} abs | 10^{6} KN/m^{2} |
| 0 | 999.8 | 9.805 | 0.001781 | 1.785 | 0.0756 | 0.611 | 2.02 |
| 5 | 1000.0 | 9.807 | 0.001518 | 1.519 | 0.0749 | 0.872 | 2.06 |
| 10 | 999.7 | 9.804 | 0.001307 | 1.306 | 0.0742 | 1.230 | 2.10 |
| 15 | 999.1 | 9.798 | 0.001139 | 1.139 | 0.0735 | 1.710 | 2.14 |
| 20 | 998.2 | 9.789 | 0.001002 | 1.003 | 0.0728 | 2.340 | 2.18 |
| 25 | 997.0 | 9.777 | 0.000890 | 0.893 | 0.0720 | 3.170 | 2.22 |
| 30 | 995.7 | 9.765 | 0.000798 | 0.800 | 0.0712 | 4.240 | 2.25 |
| 40 | 992.2 | 9.731 | 0.000653 | 0.658 | 0.0696 | 7.380 | 2.28 |
| 50 | 988.0 | 9.690 | 0.000547 | 0.553 | 0.0679 | 12.330 | 2.29 |
| 60 | 983.2 | 9.642 | 0.000466 | 0.474 | 0.0662 | 19.920 | 2.28 |
| 70 | 977.8 | 9.589 | 0.000404 | 0.413 | 0.0644 | 31.160 | 2.25 |
| 80 | 971.8 | 9.530 | 0.000354 | 0.364 | 0.0626 | 47.340 | 2.20 |
| 90 | 965.3 | 9.467 | 0.000315 | 0.326 | 0.0608 | 70.100 | 2.14 |
| 100 | 958.4 | 9.399 | 0.000282 | 0.294 | 0.0589 | 101.330 | 2.07 |
| Table 11.1 | ||||
| Similitude Scale Ratios for Physical Quantities for a Pressure Model | ||||
| Physical Quantity |
FLT System |
MLT System |
Primary Scale Ratios | Secondary/Similitude Scale Ratios for a Pressure Model |
| F_{r} = \frac{F_{p_{p}}}{F_{p_{m}}} = \frac{F_{I_{p}}}{F_{I_{m}}} = constant | \underbrace{\left[\left(\frac{\rho v^{2}}{\Delta p} \right)_{p} \right] }_{E_{p}} = \underbrace{\left[\left(\frac{\rho v^{2}}{\Delta p} \right)_{m} \right] }_{E_{m}} | |||
| Geometrics Length, L |
L | L | L_{r} = \frac{L_{p}}{L_{m}} | L_{r} = \frac{L_{p}}{L_{m}} |
| Area, A | L^{2} | L^{2} | L_{r}^{2} = \frac{L_{p}^{2}}{L_{m}^{2}} | L_{r}^{2} = \frac{L_{p}^{2}}{L_{m}^{2}} |
| Volume, V | L^{3} | L^{3} | L_{r}^{3} = \frac{L_{p}^{3}}{L_{m}^{3}} | L_{r}^{3} = \frac{L_{p}^{3}}{L_{m}^{3}} |
| Kinematics Time, T |
T | T | T_{r} = \frac{L_{r}}{v_{r}} | T_{r} = \frac{L_{r}}{v_{r}} = L_{r} \Delta p_{r}^{-1/2} \rho _{r}^{1/2} |
| Velocity, v | LT^{-1} | LT^{-1} | v_{r} = \frac{v_{p}}{v_{m}} | v_{r} = \frac{v_{p}}{v_{m}} = \frac{\left(\sqrt{\frac{\Delta p}{\rho } } \right)_{p} }{\left(\sqrt{\frac{\Delta p}{\rho } } \right)_{m} } = \Delta p_{r}^{1/2} \rho _{r}^{-1/2} |
| Acceleration, a | LT^{-2} | LT^{-2} | a_{r} = \frac{L_{r}}{T_{r}^{2}} = \frac{v_{r}^{2}}{L_{r}} | a_{r} = \frac{v_{r}^{2}}{L_{r}} = \Delta p_{r} \rho _{r}^{-1} L_{r}^{-1} |
| Discharge, Q | L^{3}T^{-1} | L^{3}T^{-1} | Q_{r} = v_{r}. L_{r}^{2} = \Delta p_{r}^{1/2} \rho _{r}^{-1/2} L_{r}^{2} | |
| Dynamics Mass, M |
FL^{-1}T^{2} | M | M_{r} = F_{r}a_{r}^{-1} = \rho _{r} L_{r}^{3} | |
| Force, F | F | MLT^{-2} | F_{r} = \frac{F_{p_{p}}}{F_{p_{m}}} = \frac{F_{I_{p}}}{F_{I_{m}}} | F_{r} = \Delta p_{r} L_{r}^{2} = \rho _{r} v^{2}_{r} L_{r}^{2} |
| Pressure, p | FL^{-2} | ML^{-1}T^{-2} | p_{r} = F_{r} L_{r}^{-2} = \Delta p_{r} = \rho _{r} v^{2}_{r} | |
| Momentum, Mv or Impulse, FT |
FT | MLT^{-1} | F_{r} T_{r} = \rho _{r}^{1/2} L_{r}^{3} \Delta p_{r}^{1/2} | |
| Energy, E or Work, W |
FL | ML^{2}T^{-2} | W_{r} = F_{r} L_{r}= \Delta p_{r} L_{r}^{3} | |
| Power, P | FLT^{-1} | ML^{2}T^{-3} | p_{r} = W_{r} T_{r}^{-1} = \Delta p_{r}^{3/2} = L^{2}_{r} \rho _{r}^{-1/2} | |
| Table A.5 | ||||||||
| Physical Properties for Some Common Gases at Standard Sea-Level Atmospheric Pressure at Room Temperature (68^{\circ }F or 20^{\circ }C ) | ||||||||
| Gas at 68^{\circ }F |
Chemical Formula |
Molar Mass (m) slug=slug- mol |
Density (ρ) slug/ft^{3} |
Absolute (Dynamic) Viscosity (μ) 10^{-6} Ib-sec/ft^{2} |
Gas Constant (R) ft-Ib/(slug-^{\circ }R )=ft^{2}/(sec^{2} -^{\circ }R ) |
Specific Heat | Specific Heat Ratio, K=C_{\rho }/C_{\upsilon } |
|
| C_{\rho } | C_{\upsilon } | |||||||
| ft-Ib/(slug-^{\circ }R )=ft^{2}/(sec^{2} -^{\circ }R ) | ||||||||
| Air | 28.960 | 0.002310 | 0.376 | 1715 | 6000 | 4285 | 1.40 | |
| Carbon dioxide | CO_{2} | 44.010 | 0.003540 | 0.310 | 1123 | 5132 | 4009 | 1.28 |
| Carbon monoxide | CO | 28.010 | 0.002260 | 0.380 | 1778 | 6218 | 4440 | 1.40 |
| Helium | He | 4.003 | 0.000323 | 0.411 | 12,420 | 13,230 | 18,810 | 1.66 |
| Hydrogen | H_{2} | 2.016 | 0.000162 | 0.189 | 24,680 | 86,390 | 61,710 | 1.40 |
| Methane | CH_{2} | 16.040 | 0.001290 | 0.280 | 3100 | 13,400 | 10,300 | 1.30 |
| Nitrogen | N_{2} | 28.020 | 0.002260 | 0.368 | 1773 | 6210 | 4437 | 1.40 |
| Oxygen | O_{2} | 32.000 | 0.002580 | 0.418 | 1554 | 5437 | 3883 | 1.40 |
| Water vapor | H_{2}O | 18.020 | 0.001450 | 0.212 | 2760 | 11,110 | 8350 | 1.33 |
| at 20^{\circ } C | kg/kg-mol | kg/m^{3} | 10^{-6} N-sec/m^{2} | N-m/(kg-^{\circ}K )=m^{2} /(sec^{2}-^{\circ}K ) | N-m/(kg-^{\circ}K )=m^{2} /(sec^{2}-^{\circ}K ) | |||
| Air | 28.960 | 1.2050 | 18.0 | 287 | 1003 | 716 | 1.40 | |
| Carbon dioxide | CO_{2} | 44.010 | 1.8400 | 14.8 | 188 | 858 | 670 | 1.28 |
| Carbon monoxide | CO | 28.010 | 1.1600 | 18.2 | 297 | 1040 | 743 | 1.40 |
| Helium | He | 4.003 | 0.1660 | 19.7 | 2077 | 5220 | 3143 | 1.66 |
| Hydrogen | H_{2} | 2.016 | 0.0839 | 9.0 | 4120 | 14,450 | 10,330 | 1.40 |
| Methane | CH_{2} | 16.040 | 0.6680 | 13.4 | 520 | 2250 | 1730 | 1.30 |
| Nitrogen | N_{2} | 28.020 | 1.1600 | 17.6 | 297 | 1040 | 743 | 1.40 |
| Oxygen | O_{2} | 32.000 | 1.3300 | 20.0 | 260 | 909 | 649 | 1.40 |
| Water vapor | H_{2}O | 18.020 | 0.7470 | 10.1 | 462 | 1862 | 1400 | 1.33 |
