Holooly Plus Logo
Holooly Plus Logo

Question 11.187E: Ambient air is at a condition of 14.7 lbf/in.^2, 95 F, 50% r...

Ambient air is at a condition of 14.7 lbf / in .^{2}, 95 F, 50% relative humidity. A steady stream of air at 14.7 lbf / in .^{2} , 73 F, 70% relative humidity, is to be produced by first cooling one stream to an appropriate temperature to condense out the proper amount of water and then mix this stream adiabatically with the second one at ambient conditions. What is the ratio of the two flow rates? To what temperature must the first stream be cooled?

The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
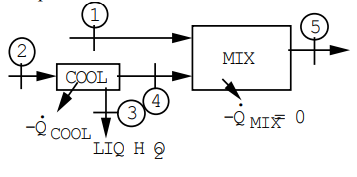
\begin{aligned}&P_{1}=P_{2}=P_{5}=14.7   lbf / in ^{2} \\&T_{1}=T_{2}=95  F \\&\phi_{1}=\phi_{2}=0.50, \phi_{4}=1.0 \\& T _{5}=73   F , \phi_{5}=0.70\end{aligned} \begin{aligned}&P_{ v 1}= P _{ v 2}=0.5 \times 0.8246=0.4123, w _{1}= w _{2}=0.622 \times \frac{0.4123}{14.7-0.4123}=0.0179 \\& P _{ v 5}=0.7 \times 0.4064=0.2845 \quad \Rightarrow \quad w _{5}=0.622 \times \frac{0.2845}{14.7-0.2845}=0.0123\end{aligned}

MIX: Call the mass flow ratio  r = m _{ a 2} / m _{ a 1}

Conservation of water mass:  w _{1}+ r w _{4}=(1+ r ) w _{5}

Energy Eq.:

\begin{aligned}h _{ a1 }+ w _{1} h _{ v1 }+ rh _{ a 4}+ rw _{4} h _{ v 4} &=(1+ r ) h _{ a 5}+(1+ r ) w _{5} h _{ v 5} \\\rightarrow & 0.0179+ rw _{4}=(1+ r ) 0.0123\end{aligned}

or

\begin{gathered}r =\frac{0.0179-0.0123}{0.0123- w _{4}}, \text { with } \quad w _{4}=0.622 \times \frac{ P _{ G 4}}{14.7- P _{ G 4}} \\\begin{aligned}0.24 \times 555+0.0179 \times 1107.2+ r \times 0.24 \times T _{4}+ rw _{4} h _{ v 4} \\=(1+ r ) \times 0.24 \times 533+(1+ r ) \times 0.0123 \times 1093.3\end{aligned}\end{gathered}

or        r \left[0.24 \times T _{4}+ w _{4} h _{ G 4}-141.4\right]+11.66=0

Assume  T _{4}=40   F \quad \rightarrow P _{ G 4}=0.12166   psia , h _{ G 4}=1078.9   Btu / lbm

\begin{aligned}& w _{4}=0.622 \times \frac{0.12166}{14.7-0.12166}=0.0052 \\&\frac{ m _{ a 2}}{ m _{ a1 }}=\frac{0.0179-0.0123}{0.0123-0.0052}= 0 . 7 8 8 7\end{aligned}

0.7887[0.24×500 + 0.0052×1078.9 – 141.4] + 11.66 = -0.29 ≈ 0 OK
=>       T _{4} = 40 F

 

187

Related Answered Questions

A large air separation plant takes in ambient air (79% N2, 21% O2 by volume) at 14.7 lbf/in.^2, 70 F, at a rate of 2 lb mol/s. It discharges a stream of pure O2 gas at 30 lbf/in.^2, 200 F, and a stream of pure N2 gas at 14.7 lbf/in.^2, 70 F. The plant operates on an electrical power input of 2000

Verified Answer:
\dot{ S }_{ gen }=-\frac{\dot{ Q }_{ CV }}{...

A mixture of 50% carbon dioxide and 50% water by mass is brought from 2800 R, 150 lbf/in.^2 to 900 R, 30 lbf/in.^2 in a polytropic process through a steady flow device. Find the necessary heat transfer and work involved using values from F.4.

Verified Answer:
Process     Pv ^{ n } = constant   ...

Weighing of masses gives a mixture at 80 F, 35 lbf/in.^2 with 1 lbm O2, 3 lbm N2 and 1 lbm CH4. Find the partial pressures of each component, the mixture specific volume (mass basis), mixture molecular weight and the total volume.

Verified Answer:
From Eq. 11.4:          y _{ i }=\left( m _...

To refresh air in a room, a counterflow heat exchanger is mounted in the wall, as shown in Fig. P11.122. It draws in outside air at 33 F, 80% relative humidity and draws room air, 104 F, 50% relative humidity, out. Assume an exchange of 6 lbm/min dry air in a steady flow device, and also that the

Verified Answer:
State 3:        P _{ g 3}=1.0804   psia , h...

An indoor pool evaporates 3 lbm/h of water, which is removed by a dehumidifier to maintain 70 F, Φ = 70% in the room. The dehumidifier is a refrigeration cycle in which air flowing over the evaporator cools such that liquid water drops out, and the air continues flowing over the condenser, as shown

Verified Answer:
The unit must remove 3 lbm/h liquid to keep steady...

A commercial laundry runs a dryer that has an exit flow of 1 lbm/s moist air at 120 F, 70% relative humidity. To save on the heating cost a counterflow stack heat exchanger is used to heat a cold water line at 50 F for the washers with the exit flow, as shown in Fig. P11.105. Assume the outgoing

Verified Answer:
Dryer oulet,   1: 120  F,  \Phi = 7...

Atmospheric air at 95 F, relative humidity of 10%, is too warm and also too dry. An air conditioner should deliver air at 70 F and 50% relative humidity in the amount of 3600 ft^3 per hour. Sketch a setup to accomplish this, find any amount of liquid (at 68 F) that is needed or discarded and any

Verified Answer:
CV air conditioner. Check first the two states, in...

A flow of moist air from a domestic furnace, state 1 in Figure P11.100, is at 120 F, 10% relative humidity with a flow rate of 0.1 lbm/s dry air. A small electric heater adds steam at 212 F, 14.7 psia generated from tap water at 60 F. Up in the living room the flow comes out at state 4: 90 F, 60%

Verified Answer:
State 1:       F.7.1:        P _{ g 1}=1.69...

Two moist air streams with 85% relative humidity, both flowing at a rate of 0.2 lbm/s of dry air are mixed in a steady flow setup. One inlet flowstream is at 90 F and the other at 61 F. Find the exit relative humidity.

Verified Answer:
CV mixing chamber. Continuity Eq. water:          ...

To save on natural gas use in the previous problem it is suggested to take and cool the mixture and condense out some water before heating it back up. So the flow is cooled from 200 F to 120 F as shown in Fig. P11.83 and the now dryer mixture is heated to 1500 F. Find the amount of water condensed

Verified Answer:
Eq.11.25:          P _{ v }=\phi P _{ g }=0...