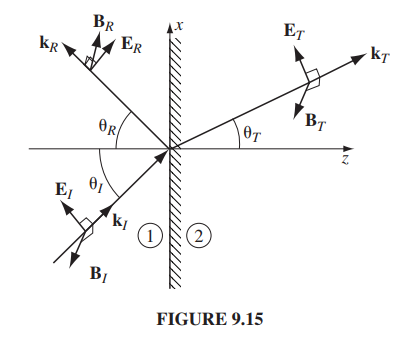
\left\{\begin{array}{l}\tilde{ E }_{I}=\tilde{E}_{0_{I}} e^{i\left( k _{I} \cdot r -\omega t\right)} \hat{ y } \\\tilde{ B }_{I}=\frac{1}{v_{1}} \tilde{E}_{0_{I}} e^{i\left( k _{I} \cdot r -\omega t\right)}\left(-\cos \theta_{1} \hat{ x }+\sin \theta_{1} \hat{ z }\right)\end{array}\right\}
\left\{\begin{array}{l}\tilde{ E }_{R}=\tilde{E}_{0_{R}} e^{i\left( k _{R} \cdot r -\omega t\right)} \hat{ y } \\\tilde{ B }_{R}=\frac{1}{v_{1}} \tilde{E}_{0_{R}} e^{i\left( k _{R} \cdot r -\omega t\right)}\left(\cos \theta_{1} \hat{ x }+\sin \theta_{1} \hat{ z }\right)\end{array}\right\}
\left\{\begin{array}{l}\tilde{ E }_{T}=\tilde{E}_{0_{T}} e^{i\left( k _{T} \cdot r -\omega t\right)} \hat{ y } \\\tilde{ B }_{T}=\frac{1}{v_{2}} \tilde{E}_{0_{T}} e^{i\left( k _{T} \cdot r -\omega t\right)}\left(-\cos \theta_{2} \hat{ x }+\sin \theta_{2} \hat{ z }\right)\end{array}\right\}
Boundary conditions: \begin{cases}\text { (i) } \epsilon_{1} E_{1}^{\perp}=\epsilon_{2} E_{2}^{\perp}, & \text { (iii) } E _{1}^{\|}= E _{2}^{\|} \\ \text {(ii) } B_{1}^{\perp}=B_{2}^{\perp}, & \text { (iv) } \frac{1}{\mu_{1}} B _{1}^{\|}=\frac{1}{\mu_{2}} B _{2}^{\|}\end{cases}
Law of refraction: \frac{\sin \theta_{2}}{\sin \theta_{1}}=\frac{v_{2}}{v_{1}} .\left[\text { Note: } k _{I} \cdot r -\omega t= k _{R} \cdot r -\omega t= k _{T} \cdot r -\omega t, \text { at } z=0\right. , so we can drop all exponential factors in applying the boundary conditions.]
Boundary condition (i): 0 = 0 (trivial). Boundary condition \text { (iii): } \tilde{E}_{0_{I}}+\tilde{E}_{0_{R}}=\tilde{E}_{0_{T}}.
Boundary condition \text { (ii): } \frac{1}{v_{1}} \tilde{E}_{0_{I}} \sin \theta_{1}+\frac{1}{v_{1}} \tilde{E}_{0_{R}} \sin \theta_{1}=\frac{1}{v_{2}} \tilde{E}_{0_{T}} \sin \theta_{2} \Rightarrow \tilde{E}_{0_{I}}+\tilde{E}_{0_{R}}=\left(\frac{v_{1} \sin \theta_{2}}{v_{2} \sin \theta_{1}}\right) \tilde{E}_{0_{T}}.
But the term in parentheses is 1, by the law of refraction, so this is the same as (iii)
Boundary condition ( iv ): \frac{1}{\mu_{1}}\left[\frac{1}{v_{1}} \tilde{E}_{0_{I}}\left(-\cos \theta_{1}\right)+\frac{1}{v_{1}} \tilde{E}_{0_{R}} \cos \theta_{1}\right]=\frac{1}{\mu_{2} v_{2}} \tilde{E}_{0_{T}}\left(-\cos \theta_{2}\right) \Rightarrow \tilde{E}_{0_{I}}-\tilde{E}_{0_{R}}=\left(\frac{\mu_{1} v_{1} \cos \theta_{2}}{\mu_{2} v_{2} \cos \theta_{1}}\right) \tilde{E}_{0_{T}} . Let \alpha \equiv \frac{\cos \theta_{2}}{\cos \theta_{1}} ; \beta \equiv \frac{\mu_{1} v_{1}}{\mu_{2} v_{2}} . Then \tilde{E}_{0_{I}}-\tilde{E}_{0_{R}}=\alpha \beta \tilde{E}_{0_{T}}.
Solving for \tilde{E}_{0_{R}} \text { and } \tilde{E}_{0_{T}}: 2 \tilde{E}_{0_{I}}=(1+\alpha \beta) \tilde{E}_{0_{T}} \Rightarrow \tilde{E}_{0_{T}}=\left(\frac{2}{1+\alpha \beta}\right) \tilde{E}_{0_{I}};
\tilde{E}_{0_{R}}=\tilde{E}_{0_{T}}-\tilde{E}_{0_{I}}=\left(\frac{2}{1+\alpha \beta}-\frac{1+\alpha \beta}{1+\alpha \beta}\right) \tilde{E}_{0_{I}} \Rightarrow \tilde{E}_{0_{R}}=\left(\frac{1-\alpha \beta}{1+\alpha \beta}\right) \tilde{E}_{0_{I}}.
Since \alpha \text { and } \beta are positive, it follows that 2 /(1+\alpha \beta) is positive, and hence the transmitted wave is in phase with the incident wave, and the (real) amplitudes are related by E_{0_{T}}=\left(\frac{2}{1+\alpha \beta}\right) E_{0_{I}} The reflected wave is in phase if \alpha \beta<1 \text { and } 180^{\circ} \text { out of phase if } \alpha \beta>1 ; the (real) amplitudes are related by E_{0_{R}}=\left|\frac{1-\alpha \beta}{1+\alpha \beta}\right| E_{0_{I}} .
These are the Fresnel equations for polarization perpendicular to the plane of incidence.
To construct the graphs, note that \alpha \beta=\beta \frac{\sqrt{1-\sin ^{2} \theta / \beta^{2}}}{\cos \theta}=\frac{\sqrt{\beta^{2}-\sin ^{2} \theta}}{\cos \theta} , where θ is the angle of incidence, so, for \beta=1.5, \alpha \beta=\frac{\sqrt{2.25-\sin ^{2} \theta}}{\cos \theta} . [In the figure, the minus signs on the vertical axis should be decimal points.]
Is there a Brewster’s angle? Well, E_{0_{R}}=0 \text { would mean that } \alpha \beta=1, and hence that
\alpha=\frac{\sqrt{1-\left(v_{2} / v_{1}\right)^{2} \sin ^{2} \theta}}{\cos \theta}=\frac{1}{\beta}=\frac{\mu_{2} v_{2}}{\mu_{1} v_{1}} \text {, or } 1-\left(\frac{v_{2}}{v_{1}}\right)^{2} \sin ^{2} \theta=\left(\frac{\mu_{2} v_{2}}{\mu_{1} v_{1}}\right)^{2} \cos ^{2} \theta , so
1=\left(\frac{v_{2}}{v_{1}}\right)^{2}\left[\sin ^{2} \theta+\left(\mu_{2} / \mu_{1}\right)^{2} \cos ^{2} \theta\right] . \text { Since } \mu_{1} \approx \mu_{2}, \text { this means } 1 \approx\left(v_{2} / v_{1}\right)^{2} , which is only true for optically
indistinguishable media, in which case there is of course no reflection—but that would be true at any angle, not just at a special “Brewster’s angle”. [If \mu_{2} were substantially different from \mu_{1} , and the relative velocities were just right, it would be possible to get a Brewster’s angle for this case, at
\left(\frac{v_{1}}{v_{2}}\right)^{2}=1-\cos ^{2} \theta+\left(\frac{\mu_{2}}{\mu_{1}}\right)^{2} \cos ^{2} \theta \Rightarrow \cos ^{2} \theta=\frac{\left(v_{1} / v_{2}\right)^{2}-1}{\left(\mu_{2} / \mu_{1}\right)^{2}-1}=\frac{\left(\mu_{2} \epsilon_{2} / \mu_{1} \epsilon_{1}\right)-1}{\left(\mu_{2} / \mu_{1}\right)^{2}-1}=\frac{\left(\epsilon_{2} / \epsilon_{1}\right)-\left(\mu_{1} / \mu_{2}\right)}{\left(\mu_{2} / \mu_{1}\right)-\left(\mu_{1} / \mu_{2}\right)}
But the media would be very peculiar.]
By the same token, \delta_{R} is either always 0, or always π, for a given interface—it does not switch over as you change θ, the way it does for polarization in the plane of incidence. In particular, if \beta=3 / 2, \text { then } \alpha \beta>1 , for
\alpha \beta=\frac{\sqrt{2.25-\sin ^{2} \theta}}{\cos \theta}>1 \text { if } 2.25-\sin ^{2} \theta>\cos ^{2} \theta, \text { or } 2.25>\sin ^{2} \theta+\cos ^{2} \theta=1.
In general, for \beta>1, \alpha \beta>1, \text { and hence } \delta_{R}=\pi \text {. For } \beta<1, \alpha \beta<1, \text { and } \delta_{R}=0 .
At normal incidence, α = 1, so Fresnel’s equations reduce to E_{0_{T}}=\left(\frac{2}{1+\beta}\right) E_{0_{I}} ; E_{0_{R}}=\left|\frac{1-\beta}{1+\beta}\right| E_{0_{I}} ,
consistent with Eq. 9.82.
\tilde{E}_{0_{R}}=\left(\frac{1-\beta}{1+\beta}\right) \tilde{E}_{0_{I}}, \quad \tilde{E}_{0_{T}}=\left(\frac{2}{1+\beta}\right) \tilde{E}_{0_{I}} (9.82)
Reflection and Transmission coe!cients: R=\left(\frac{E_{0_{R}}}{E_{0_{I}}}\right)^{2}=\left(\frac{1-\alpha \beta}{1+\alpha \beta}\right)^{2} . Referring to Eq. 9.116,
T \equiv \frac{I_{T}}{I_{I}}=\frac{\epsilon_{2} v_{2}}{\epsilon_{1} v_{1}}\left(\frac{E_{0_{T}}}{E_{0_{I}}}\right)^{2} \frac{\cos \theta_{T}}{\cos \theta_{I}}=\alpha \beta\left(\frac{2}{\alpha+\beta}\right)^{2} (9.116)
T=\frac{\epsilon_{2} v_{2}}{\epsilon_{1} v_{1}} \alpha\left(\frac{E_{0_{T}}}{E_{0_{I}}}\right)^{2}=\alpha \beta\left(\frac{2}{1+\alpha \beta}\right)^{2}.
R+T=\frac{(1-\alpha \beta)^{2}+4 \alpha \beta}{(1+\alpha \beta)^{2}}=\frac{1-2 \alpha \beta+\alpha^{2} \beta^{2}+4 \alpha \beta}{(1+\alpha \beta)^{2}}=\frac{(1+\alpha \beta)^{2}}{(1+\alpha \beta)^{2}}=1.