(a) For the forced cross flow, we use the correlation in Table, i.e.,
\left\langle Nu\right\rangle _{D}=a_{1}Re^{a_{2}}Pr^{1/3}, Re_{D}=\frac{u_{f,\infty }D}{v_{f}}
The constants a_{1} and a_{2} depend on Re_{D} as shown in Table . From \left\langle Q_{ku}\right\rangle _{L( or D)}=\frac{T_{s}-T_{f,\infty }}{\left\langle R_{ku}\right\rangle_{L(or D)} } =A_{ku}\frac{k_{f}}{L(or D)}\left\langle Nu\right\rangle _{L(or D)}(T_{s}-T_{f,\infty }), Re_{L(or D)}=\frac{u_{f,\infty }L(or D)}{v_{f}} , we have for A_{ku}\left\langle R_{ku}\right\rangle _{D}
A_{ku}\left\langle R_{ku}\right\rangle _{ D}=\frac{T_{s}-T_{f,\infty }}{ q_{ku}} =\frac{D}{\left\langle Nu\right\rangle _{D}k_{f}}
For water, at T = 330 K, from Table we have
ν_{f} = 5.05 × 10^{−7} m^{2}/s
k_{f} = 0.648 W/m-K
Pr = 3.22.
(b) For the thermobuoyant flow, we use the correlation in Table , i.e.,
\left\langle Nu\right\rangle _{D}=(\left\langle Nu _{D,l}\right\rangle^{3.3}+ \left\langle Nu_{D,t}\right\rangle ^{3.3})^{1/3.3}
\left\langle Nu _{D,l}\right\rangle=\frac{1.6}{ln[1 + 1.6(0.772a_{1}Ra^{1/4}_{ D} )]}
\left\langle Nu _{D,t}\right\rangle=\frac{0.13Pr^{0.22}}{(1 + 0.61Pr^{0.81})^{0.42} } Ra_{D}^{1/3}
a_{1}=\frac{4}{3}\frac{0.503}{[1 + (0.492/Pr)^{9/16}]^{ 4/9}}
Ra_{D}=\frac{g\beta _{f}(T_{s}-T_{f,\infty })D^{3}}{v_{f}\alpha _{f}}
Again
A_{ku}\left\langle R_{ku}\right\rangle _{D}=\frac{D}{\left\langle Nu\right\rangle_{D}k_{f} }
For water, at T = 325 K, from Table, we have
β_{f} = 0.000203 1/K available only at T = 290 K
α_{f} = 1.57 × 10^{−7} m^{2}/s.
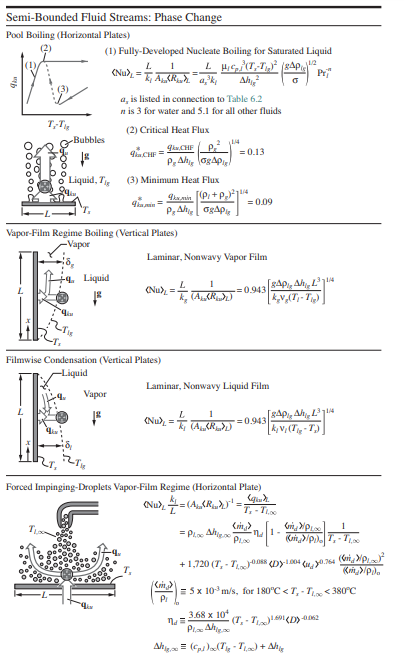
(c) For the pool nucleate boiling, we use the correlation in Table. Here we directly write for A_{ku}\left\langle R_{ku}\right\rangle _{D} as
\frac{1}{A_{ku}\left\langle R_{ku}\right\rangle _{D}} =\frac{1}{a_{s}^{3}}\frac{\mu _{l}c_{p,l}^{3}(T_{s}-T_{lg})^{2}}{\Delta h_{lg}^{2}}\left(\frac{g\Delta \rho _{lg}}{\sigma } \right) ^{1/2}Pr_{l}^{-n}
From Table 6.5, for water we have n = 3, and we choose a water-copper pair that gives a_{s} = 0.013 from Table.
For water at T = 373 K, from Table we have
μ_{l} = 2.775 × 10^{−4} Pa-s
c_{p,l} = 4,220 J/kg-K
\Delta h_{lg} = 2.567 × 10^{6} J/kg
\Delta ρ_{lg} = (958.3 − 0.597)( kg/m^{3}) = 957.7 kg/m^{3}
\sigma= 0.05891 N/m
Pr_{l} = 1.73
g = 9.807 m/s^{2}.
Figure shows the variation of A_{ku}\left\langle R_{ku}\right\rangle _{D} for the three flows. The forced cross flow is shown to the left with u_{f,∞} as the variable. The thermobuoyant and pool nucleate boiling results are shown to the right, with T_{s} − T_{f,∞} as the variable. The results for both diameters are shown.
Note that forced flow and nucleate boiling both result in a A_{ku}\left\langle R_{ku}\right\rangle _{D} that is small compared to the thermobuoyant flow. For forced flow, a yet lower resistance can be obtained by further increasing the water velocity (the sonic velocity in water is about 1,500 m/s). The highest velocity used is based on the range of validity of the correlation.