Question 8.182E: Calculate the irreversibility for the process described in P...

C.V. Cylinder volume out to T _{ o } = 61 F.

Continuity Eq.4.15:        m _{2}- m _{1}= m _{ in }

Energy Eq.4.16:              m _{2} u _{2}- m _{1} u _{1}= m _{ in } h _{\text {line }}+{ }_{1} Q _{2}-{ }_{1} W _{2}

Entropy Eq.7.12:            m _{2} s _{2}- m _{1} s _{1}= m _{ i } s _{ i }+{ }_{1} Q _{2} / T _{ o }+{ }_{1} S _{2  gen}

Process:        P _{1}  is constant to stops, then constant V to state 2 at  P _{2}

State 1:      P _{1}, T _{1} \quad m _{1}=\frac{ P _{1} V }{ RT _{1}}=\frac{45 \times 9 \times 144}{53.34 \times 519.7}=2.104   lbm

State 2:
Open to 60   lbf / in ^{2}, T _{2}=630   R

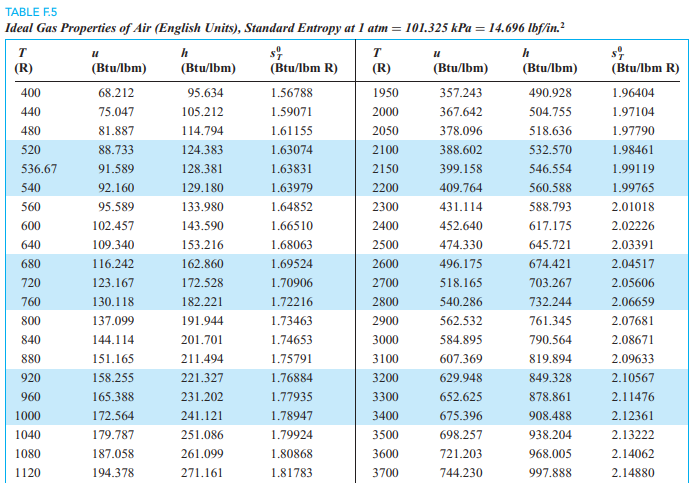
Table F.5:

Only work as piston moves (V changes) while  P = P _{1} \text { until } V = V _{\text {stop }}

Use from table F.4:      C _{ p }=0.24,     R =53.34 / 778=0.06856   Btu / lbm  R,

……………………………………..

Eq.4.15 : 1=\frac{\dot{m}_{1}}{\dot{m}_{3}}+\frac{\dot{m}_{2}}{\dot{m}_{3}}

Eq.4.16 : 0=\frac{\dot{m}_{1}}{\dot{m}_{3}} h_{1}+\frac{\dot{m}_{2}}{\dot{m}_{3}} h_{2}-h_{3}+\dot{Q} / \dot{m}_{3}

Eq.7.12 : \left(m_{2} s_{2}-m_{1} s_{1}\right)_{ c . v .}=\sum m_{i} s_{i}-\sum m_{e} s_{e}+\int_{0}^{t} \sum_{ c.s. } \frac{\dot{Q}_{ c.v. }}{T} d t+{ }_{1} S_{2 gen }