Compute the true stress and the logarithmic strain using the data of Prob. 2–6 and plot the results on log-log paper. Then find the plastic strength coefficient

Question

Compute the true stress and the logarithmic strain using the data of Prob. 2-6 and plot the results on log-log paper. Then find the plastic strength coefficient [latex]\sigma_{0}[/latex] and the strain-strengthening exponent [latex]m[/latex]. Find also the yield strength and the ultimate strength after the specimen has had 20 percent cold work.

Accepted Answer

To plot [latex]\sigma_{ ext {true }}[/latex] vs. [latex]\varepsilon[/latex], the following equations are applied to the data.

[latex]\sigma_{ ext {troe }}=\frac{P}{A}[/latex]

Eq. (2-4)

[latex]\begin{aligned}&\varepsilon=\ln \frac{l}{l_{0}} \quad ext { for } 0 \leq \Delta l \leq 0.0028 ext { in } \&\varepsilon=\ln \frac{A_{0}}{A} \quad ext { for } \Delta l>0.0028 ext { in }\end{aligned}[/latex]

where [latex]A_{0}=\frac{\pi(0.503)^{2}}{4}=0.1987 \mathrm{in}^{2}[/latex]

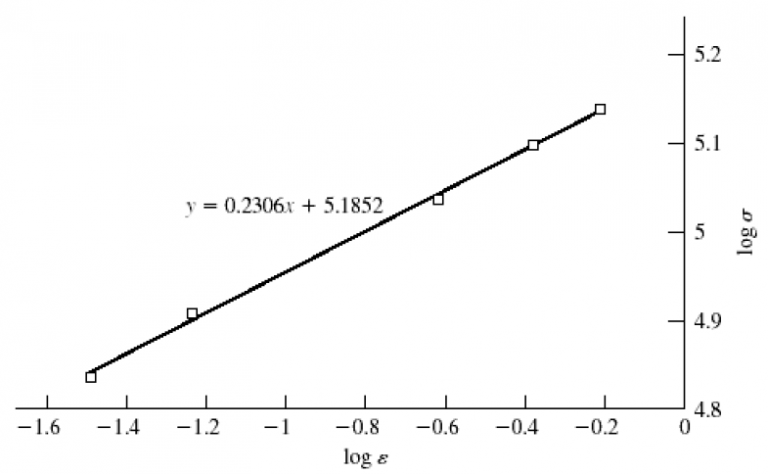
The results are summarized in the table below and plotted on the next page. The last 5 points of data are used to plot [latex]\log \sigma[/latex] vs [latex]\log \varepsilon[/latex]

The curve fit gives [latex]m=0.2306[/latex]

[latex]\log \sigma_{0}=5.1852 \Rightarrow \sigma_{0}=153.2 \mathrm{kpsi} [/latex]

For [latex]20 \%[/latex] cold work, Eq. (2-14) and Eq. (2-17) give,

[latex]\begin{gathered}A=A_{0}(1-W)=0.1987(1-0.2)=0.1590 \mathrm{in}^{2} \\varepsilon=\ln \frac{A_{0}}{A}=\ln \frac{0.1987}{0.1590}=0.2231\end{gathered}[/latex]

Eq. [latex](2-18): S_{y^{\prime}}=\sigma_{0} \varepsilon^{m}=153.2(0.2231)^{0.2306}=108.4 \mathrm{kpsi} \quad [/latex]

Eq. [latex](2-19)[/latex], with [latex]S_{u}=85.6[/latex] from Prob. 2-6,

[latex]S_{u}^{\prime}=\frac{S_{u}}{1-W}=\frac{85.6}{1-0.2}=107 \mathrm{kpsi} \quad[/latex]

Eq. (2-14),

[latex]A_{i}^{\prime}=A_{0}(1-W)[/latex]

Eq (2-17),

[latex]\varepsilon=\ln \frac{l}{l_{0}}=\ln \frac{A_{0}}{A}[/latex]

Eq. (2-18),

[latex]S_{y}^{\prime}=\frac{P_{i}}{A_{i}^{\prime}}=\sigma_{0} \varepsilon_{i}^{m} \quad P_{i} \leq P_{u}[/latex]

Eq. (2-19),

[latex]S_{u}^{\prime}=\frac{S_{u} A_{0}}{A_{0}(1-W)}=\frac{S_{u}}{1-W} \quad \varepsilon_{i} \leq \varepsilon_{u}[/latex]

Eq. (2-4):

[latex]\varepsilon=\int_{l_{0}}^{l} \frac{d l}{l}=\ln \frac{l}{l_{0}}[/latex]

[latex]P[/latex]	[latex]\Delta L[/latex]	[latex]A [/latex]	[latex]\varepsilon [/latex]	[latex]\sigma ext { true } [/latex]	[latex]\log \varepsilon [/latex]	[latex]\log \sigma_{ ext {true }}[/latex]
0	0	0.198713	0	0
1000	0.0004	0.198713	0.0002	5032.388	-3.69901	3.70177
2000	0.0006	0.198713	0.0003	10064.78	-3.52294	4.0028
3000	0.001	0.198713	0.0005	15097.17	-3.30114	4.1789
4000	0.0013	0.198713	0.00065	20129.55	-3.18723	4.30383
7000	0.0023	0.198713	0.001149	35226.72	-2.93955	4.54687
8400	0.0028	0.198713	0.001399	42272.06	-2.85418	4.62605
8800	0.0036	0.1984	0.001575	44354.84	-2.80261	4.64694
9200	0.0089	0.1978	0.004604	46511.63	-2.33685	4.66756
9100		0.1963	0.012216	46357.62	-1.91305	4.66612
13200		0.1924	0.032284	68607.07	-1.49101	4.83637
15200		0.1875	0.058082	81066.67	-1.23596	4.90884
17000		0.1563	0.240083	108765.2	-0.61964	5.03649
16400		0.1307	0.418956	125478.2	-0.37783	5.09857
14800		0.1077	0.612511	137418.8	-0.21289	5.13805

Question 2.7: Compute the true stress and the logarithmic strain using th...

Related Answered Questions