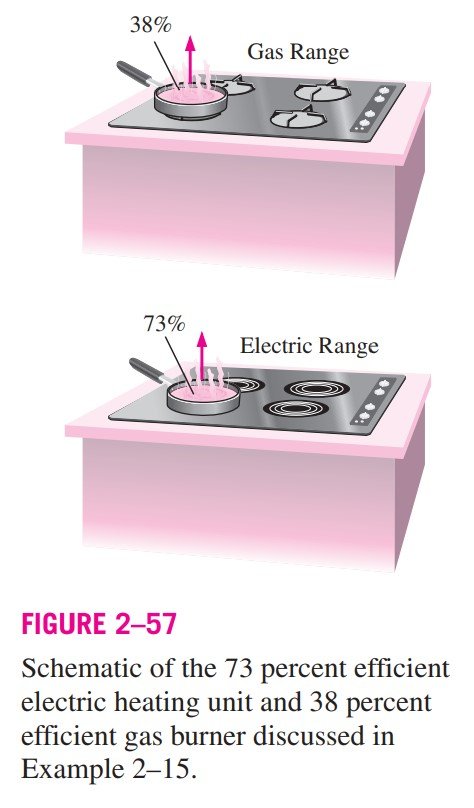
Cost of Cooking with Electric and Gas Ranges The efficiency of cooking appliances affects the internal heat gain from them since an inefficient appliance consumes a greater amount of energy for the same task, and the excess energy consumed shows up as heat in the living space. The efficiency of

Question

Cost of Cooking with Electric and Gas Ranges The efficiency of cooking appliances affects the internal heat gain from them since an inefficient appliance consumes a greater amount of energy for the same task, and the excess energy consumed shows up as heat in the living space. The efficiency of open burners is determined to be 73 percent for electric units and 38 percent for gas units (Fig. 2–57). Consider a 2-kW electric burner at a location where the unit costs of electricity and natural gas are $0.09/kWh and $0.55/therm, respectively. Determine the rate of energy consumption by the burner and the unit cost of utilized energy for both electric and gas burners.

Accepted Answer

The operation of electric and gas ranges is considered. The rate of energy consumption and the unit cost of utilized energy are to be determined.
Analysis The efficiency of the electric heater is given to be 73 percent.
Therefore, a burner that consumes 2 kW of electrical energy will supply

[latex] \dot{Q}_{ ext {utilized }}=( ext { Energy input }) imes( ext { Efficiency })=(2 kW )(0.73)= 1 . 4 6 ~ k W [/latex]

of useful energy. The unit cost of utilized energy is inversely proportional to the efficiency, and is determined from

[latex] ext { Cost of utilized energy }=\frac{ ext { Cost of energy input }}{ ext { Efficiency }}=\frac{\$ 0.09 / kWh }{0.73}=\$ 0 . 1 2 3 / k W h [/latex]

Noting that the efficiency of a gas burner is 38 percent, the energy input to a gas burner that supplies utilized energy at the same rate (1.46 kW) is

[latex] \dot{Q}_{ ext {input, gas }}=\frac{\dot{Q}_{ ext {utilized }}}{ ext { Efficiency }}=\frac{1.46 kW }{0.38}=3.84 kW \quad(=13,100 Btu / h ) [/latex]

since 1 kW = 3412 Btu/h. Therefore, a gas burner should have a rating of at least 13,100 Btu/h to perform as well as the electric unit.
Noting that 1 therm = 29.3 kWh, the unit cost of utilized energy in the case of a gas burner is determined to be

[latex] \begin{aligned} ext { Cost of utilized energy } &=\frac{ ext { Cost of energy input }}{ ext { Efficiency }}=\frac{\$ 0.55 / 29.3 kWh }{0.38} \&=\$ 0 . 0 4 9 / k W h\end{aligned}[/latex]

Discussion The cost of utilized gas is less than half of the unit cost of utilized electricity. Therefore, despite its higher efficiency, cooking with an electric burner will cost more than twice as much compared to a gas burner in this case. This explains why cost-conscious consumers always ask for gas appliances, and it is not wise to use electricity for heating purposes.

Question 2.15: Cost of Cooking with Electric and Gas Ranges The efficiency ...

This Question has been Answered.

Already have an account?

Login

Related Answered Questions