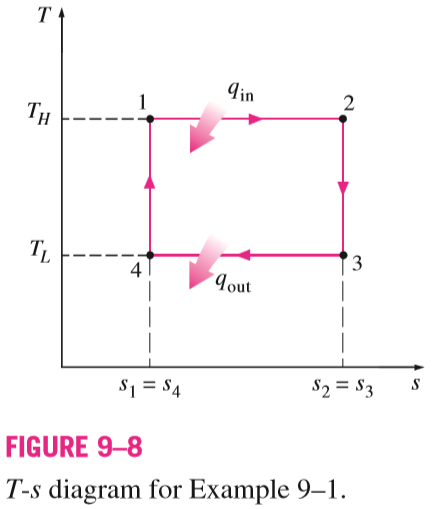
Derivation of the Efficiency of the Carnot Cycle
Show that the thermal efficiency of a Carnot cycle operating between the temperature limits of T_{H} \text { and } T_{L} is solely a function of these two temperatures and is given by Eq. 9–2.
\eta_{ th , Carnot }=1-\frac{T_{L}}{T_{H}}
It is to be shown that the efficiency of a Carnot cycle depends on the source and sink temperatures alone.
Analysis The T-s diagram of a Carnot cycle is redrawn in Fig. 9–8. All four processes that comprise the Carnot cycle are reversible, and thus the area under each process curve represents the heat transfer for that process. Heat is transferred to the system during process 1-2 and rejected during process 3-4. Therefore, the amount of heat input and heat output for the cycle can be expressed as
q_{\text {in }}=T_{H}\left(s_{2}-s_{1}\right) \quad \text { and } \quad q_{\text {out }}=T_{L}\left(s_{3}-s_{4}\right)=T_{L}\left(s_{2}-s_{1}\right)
since processes 2-3 and 4-1 are isentropic, and thus s_{2}=s_{3} \text { and } s_{4}=s_{1} . Substituting these into Eq. 9–1, we see that the thermal efficiency of a Carnot cycle is
\eta_{ th }=\frac{W_{ net }}{Q_{ in }} \quad \text { or } \quad \eta_{ th }=\frac{w_{ net }}{q_{ in }}
\eta_{ th }=\frac{w_{ net }}{q_{ in }}=1-\frac{q_{ out }}{q_{ in }}=1-\frac{T_{L}\left(s_{2}-s_{1}\right)}{T_{H}\left(s_{2}-s_{1}\right)}=1-\frac{T_{L}}{T_{H}}
Discussion Notice that the thermal efficiency of a Carnot cycle is independent of the type of the working fluid used (an ideal gas, steam, etc.) or whether the cycle is executed in a closed or steady-flow system.
