Design a 4:1 spur-gear reduction for a 100-hp, three-phase squirrel-cage induction motor running at 1120 rev/min. The load is smooth, providing a reliability of 0.95 at 10^9 revolutions of the pinion. Gearing space is meager. Use Nitralloy 135M, grade 1 material to keep the gear size small. The

Question

Design a 4:1 spur-gear reduction for a 100-hp, three-phase squirrel-cage induction motor running at 1120 rev/min. The load is smooth, providing a reliability of 0.95 at [latex]10^{9}[/latex] revolutions of the pinion. Gearing space is meager. Use Nitralloy 135M, grade 1 material to keep the gear size small. The gears are heat-treated first then nitrided.

Accepted Answer

Make the a priori decisions:

Function: 100 hp, 1120 rev/min, [latex]R=0.95, N=10^{9} ext { cycles, } K_{o}=1[/latex]

• Design factor for unquantifiable exingencies: [latex]n_{d}=2[/latex]

• Tooth system: [latex]\phi_{n}=20^{\circ}[/latex]

• Tooth count: [latex]N_{P}=18 ext { teeth, } N_{G}=72[/latex] teeth (no interference)

• Quality number: [latex]Q_{v}=6[/latex], use grade 1 material

• Assume [latex]m_{B} \geq 1.2 ext { in Eq. (14-40), } K_{B}=1[/latex]

Pitch: Select a trial diametral pitch of [latex]P_{d}=4[/latex] teeth/in. Thus, [latex]d_{p}=18 / 4=4.5[/latex] in and [latex]d_{G}=72 / 4=18[/latex] in. From Table 14–2, [latex]Y_{P}=0.309, Y_{G}=0.4324[/latex] (interpolated). From Fig. 14–6, [latex]J_{P}=0.32, J_{G}=0.415[/latex]

Table 14–2 Values of the Lewis Form Factor Y (TheseValues Are for a Normal Pressure Angle of 20°, Full-Depth Teeth, and a Diametral Pitch of Unity in the Plane of Rotation)
Number of Teeth	Y	Number of Teeth	Y
12	0.245	28	0.353
13	0.261	30	0.359
14	0.277	34	0.371
15	0.29	38	0.384
16	0.296	43	0.397
17	0.303	50	0.409
18	0.309	60	0.422
19	0.314	75	0.435
20	0.322	100	0.447
21	0.328	150	0.46
22	0.331	300	0.472
24	0.337	400	0.48
26	0.346	Rack	0.485

[latex]V=\frac{\pi d_{P} n_{P}}{12}=\frac{\pi(4.5) 1120}{12}=1319 ft / min[/latex]

[latex]W^{t}=\frac{33000 H}{V}=\frac{33000(100)}{1319}=2502 lbf[/latex]

From Eqs. (14–28) and (14–27),

[latex]\begin{array}{l}A=50+56(1-B) \B=0.25\left(12-Q_{v} ight)^{2 / 3}\end{array}[/latex] (14–28)

[latex]K_{v}=\left\{\begin{array}{ll}\left(\frac{A+\sqrt{V}}{A} ight)^{B} & V ext { in } ft / min \\left(\frac{A+\sqrt{200 V}}{A} ight)^{B} & V ext { in } m / s\end{array} ight.[/latex] (14–27)

[latex]B=0.25\left(12-Q_{v} ight)^{2 / 3}=0.25(12-6)^{2 / 3}=0.8255[/latex]

[latex]A=50+56(1-0.8255)=59.77[/latex]

[latex]K_{v}=\left(\frac{59.77+\sqrt{1319}}{59.77} ight)^{0.8255}=1.480[/latex]

From Eq. (14–38), [latex]K_{R}=0.658-0.0759 \ln (1-0.95)=0.885[/latex]. From Fig. 14–14,

[latex]K_{R}=\left\{\begin{array}{ll}0.658-0.0759 \ln (1-R) & 0.5

[latex]\left(Y_{N} ight)_{p}=1.3558\left(10^{9} ight)^{-0.0178}=0.938[/latex]

[latex]\left(Y_{N} ight)_{G}=1.3558\left(10^{9} / 4 ight)^{-0.0178}=0.961[/latex]

From Fig. 14–15,

[latex]\left(Z_{N} ight)_{P}=1.4488\left(10^{9} ight)^{-0.023}=0.900[/latex]

[latex]\left(Z_{N} ight)_{G}=1.4488\left(10^{9} / 4 ight)^{-0.023}=0.929[/latex]

From the recommendation after Eq. (14–8), 3p ≤ F ≤ 5p. Try F = 4p = 4π/P = 4π/4 = 3.14 in. From Eq. (a), Sec. 14–10,

[latex]\sigma=\frac{K_{v} W^{t}}{F m Y}[/latex] (14–8)

[latex]\sigma=\frac{M}{I / c}=\frac{6 W^{t} l}{F t^{2}}[/latex] (a)

[latex]K_{s}=1.192\left(\frac{F \sqrt{Y}}{P} ight)^{0.0535}=1.192\left(\frac{3.14 \sqrt{0.309}}{4} ight)^{0.0535}=1.140[/latex]

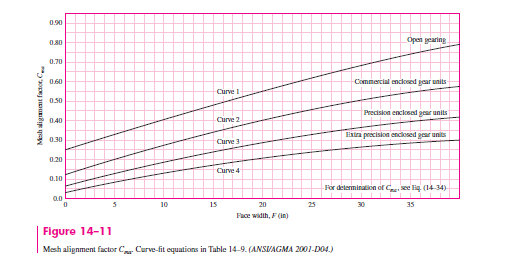
From Eqs. (14–31), (14–33) and (14–35), [latex]C_{m c}=C_{p m}=C_{e}=1[/latex]. From Fig. 14–11, [latex]C_{m a}=0.175[/latex] for commercial enclosed gear units. From Eq. (14–32), [latex]F /\left(10 d_{P} ight)=3.14 /[/latex] [10(4.5)] = 0.0698. Thus,

[latex]C_{m c}=\left\{\begin{array}{ll}1 & ext { for uncrowned teeth } \0.8 & ext { for crowned teeth }\end{array} ight.[/latex] (14–31)

[latex]C_{p m}=\left\{\begin{array}{ll}1 & ext { for straddle-mounted pinion with } S_{1} / S<0.175 \1.1 & ext { for straddle-mounted pinion with } S_{1} / S \geq 0.175\end{array} ight.[/latex] (14–33)

[latex]C_{e}=\left\{\begin{array}{cl}0.8 & ext { for gearing adjusted at assembly, or compatibility } \1 & ext { is improved by lapping, or both } \ ext { for all other conditions }\end{array} ight.[/latex] (14–35)

[latex]C_{p f}=\left\{\begin{array}{ll}\frac{F}{10 d}-0.025 & F \leq 1 ext { in } \\frac{F}{10 d}-0.0375+0.0125 F & 1

From Eq. (14–30),

[latex]K_{m}=C_{m f}=1+C_{m c}\left(C_{p f} C_{p m}+C_{m a} C_{e} ight)[/latex] (14–30)

[latex]K_{m}=1+(1)[0.0715(1)+0.175(1)]=1.247[/latex]

From Table 14–8, for steel gears, [latex]C_{p}=2300 \sqrt{ psi }[/latex]. From Eq. (14–23), with [latex]m_{G}=4[/latex] and [latex]m_{N}=1[/latex]

Table 14–8 Elastic Coefficient [latex]C_{p}\left(Z_{E} ight), \sqrt{ psi }(\sqrt{ MPa })[/latex] Source: AGMA 218.01
Gear Material and Modulus of Elasticity [latex]E_{G}, lbf / in ^{2}( MPa )^{*}[/latex]
Pinion Material	Pinion Modulus of [latex]\begin{array}{l} ext { Elasticity Ep }\ ext { psi (MPa) * }\end{array}[/latex]	Steel [latex]\begin{array}{l}30 imes 10^{6} \\left(2 imes 10^{5} ight)\end{array}[/latex]	Malleable Iron [latex]\begin{array}{c}25 imes 10^{6} \\left(1.7 imes 10^{5} ight)\end{array}[/latex]	Nodular Iron [latex]\begin{array}{c}24 imes 10^{6} \\left(1.7 imes 10^{5} ight)\end{array}[/latex]	Cast Iron [latex]\begin{array}{r}22 imes 10^{6} \\left(1.5 imes 10^{5} ight)\end{array}[/latex]	Aluminum Bronze [latex]\begin{array}{r}17.5 imes 10^{6} \\left(1.2 imes 10^{5} ight)\end{array}[/latex]	Tin Bronze [latex]\begin{array}{c}16 imes 10^{6} \\left(1.1 imes 10^{5} ight)\end{array}[/latex]
Steel	[latex]30 imes 10^{6}[/latex]	2300	2180	2160	2100	1950	1900
	[latex]\left(2 imes 10^{5} ight)[/latex]	(191)	(181)	(179)	(174)	(162)	(158)
Malleable iron	[latex]25 imes 10^{6}[/latex]	2180	2090	2070	2020	1900	1850
	[latex]\left(1.7 imes 10^{5} ight)[/latex]	(181)	(174)	(172)	(168)	(158)	(154)
Nodular iron	[latex]24 imes 10^{6}[/latex]	2160	2070	2050	2000	1880	1830
	[latex]\left(1.7 imes 10^{5} ight)[/latex]	(179)	(172)	(170)	(166)	(156)	(152)
Cast iron	[latex]22 imes 10^{6}[/latex]	2100	2020	2000	1960	1850	1800
	[latex]\left(1.5 imes 10^{5} ight)[/latex]	(174)	(168)	(166)	(163)	(154)	(149)
Aluminum bronze	[latex]17.5 imes 10^{6}[/latex]	1950	1900	1880	1850	1750	1700
	[latex]\left(1.2 imes 10^{5} ight)[/latex]	(162)	(158)	(156)	(154)	(145)	(141)
Tin bronze	[latex]16 imes 10^{6}[/latex]	1900	1850	1830	1800	1700	1650
	[latex]\left(1.1 imes 10^{5} ight)[/latex]	(158)	(154)	(152)	(149)	(141)	(137)

[latex]I=\left\{\begin{array}{ll}\frac{\cos \phi_{t} \sin \phi_{t}}{2 m_{N}} \frac{m_{G}}{m_{G}+1} & ext { external gears } \\frac{\cos \phi_{t} \sin \phi_{t}}{2 m_{N}} \frac{m_{G}}{m_{G}-1} & ext { internal gears }\end{array} ight.[/latex] (14–23)

[latex]I=\frac{\cos 20^{\circ} \sin 20^{\circ}}{2} \frac{4}{4+1}=0.1286[/latex]

Pinion tooth bending. With the above estimates of [latex]K_{s} ext { and } K_{m}[/latex] from the trial diametral pitch, we check to see if the mesh width F is controlled by bending or wear considerations. Equating Eqs. (14–15) and (14–17), substituting [latex]n_{d} W^{t} ext { for } W^{t}[/latex] , and solving for the face width [latex](F)_{ ext {bend }}[/latex] necessary to resist bending fatigue, we obtain

[latex]\sigma=\left\{\begin{array}{ll}W^{t} K_{o} K_{v} K_{s} \frac{P_{d}}{F} \frac{K_{m} K_{B}}{J} & ext { (U.S. customary units) } \W^{t} K_{o} K_{v} K_{s} \frac{1}{b m_{t}} \frac{K_{H} K_{B}}{Y_{J}} & ext { (SI units) }\end{array} ight.[/latex] (14–15)

[latex]\sigma_{ ext {all }}=\left\{\begin{array}{ll}\frac{S_{t}}{S_{F}} \frac{Y_{N}}{K_{T} K_{R}} & ext { (U.S. customary units) } \\frac{S_{t}}{S_{F}} \frac{Y_{N}}{Y_{ heta} Y_{Z}} & ext { (SI units) }\end{array} ight.[/latex] (14–17)

[latex](F)_{ ext {bend }}=n_{d} W^{t} K_{o} K_{v} K_{s} P_{d} \frac{K_{m} K_{B}}{J_{P}} \frac{K_{T} K_{R}}{S_{t} Y_{N}}[/latex] (1)

Equating Eqs. (14–16) and (14–18), substituting [latex]n_{d} W^{t} ext { for } W^{t}[/latex], and solving for the face width [latex](F)_{ ext {wear }}[/latex] necessary to resist wear fatigue, we obtain

[latex]\sigma_{c}=\left\{\begin{array}{ll}C_{p} \sqrt{W^{t} K_{o} K_{v} K_{s} \frac{K_{m}}{d_{P} F} \frac{C_{f}}{I}} & ext { (U.S. customary units) } \Z_{E} \sqrt{W^{t} K_{o} K_{v} K_{s} \frac{K_{H}}{d_{w 1} b} \frac{Z_{R}}{Z_{I}}} & ext { (SI units) }\end{array} ight.[/latex] (14–16)

[latex]\sigma_{c, ext { all }}=\left\{\begin{array}{ll}\frac{S_{c}}{S_{H}} \frac{Z_{N} C_{H}}{K_{T} K_{R}} & ext { (U.S. customary units) } \\frac{S_{c}}{S_{H}} \frac{Z_{N} Z_{W}}{Y_{ heta} Y_{Z}} & ext { (SI units) }\end{array} ight.[/latex] (14–18)

[latex](F)_{ ext {wear }}=\left(\frac{C_{p} Z_{N}}{S_{c} K_{T} K_{R}} ight)^{2} n_{d} W^{t} K_{o} K_{v} K_{s} \frac{K_{m} C_{f}}{d_{P} I}[/latex] (2)

From Table 14–5 the hardness range of Nitralloy 135M is Rockwell C32–36 (302–335 Brinell). Choosing a midrange hardness as attainable, using 320 Brinell. From Fig. 14–4,

Table 14–5 Nominal Temperature Used in Nitriding and Hardnesses Obtained Source: Darle W. Dudley, Handbook of Practical Gear Design, rev. ed., McGraw-Hill, New York, 1984.
Steel	Temperature Before Nitriding, °F	Nitriding, °F	Hardness, Rockwell C Scale
Steel	Temperature Before Nitriding, °F	Nitriding, °F	Case	Core
[latex] ext { Nitralloy } 135^{*}[/latex]	1150	975	62–65	30–35
Nitralloy 135M	1150	975	62–65	32–36
Nitralloy N	1000	975	62–65	40–44
AISI 4340	1100	975	48–53	27–35
AISI 4140	1100	975	49–54	27–35
31 Cr Mo V 9	1100	975	58–62	27–33

[latex]S_{t}=86.2(320)+12730=40310 psi[/latex]

Inserting the numerical value of [latex]S_{t}[/latex] in Eq. (1) to estimate the face width gives

[latex](F)_{ ext {bend }}=2(2502)(1) 1.48(1.14) 4 \frac{1.247(1)(1) 0.885}{0.32(40310) 0.938}=3.08 ext { in }[/latex]

From Table 14–6 for Nitralloy 135M, [latex]S_{c}=170000[/latex] psi. Inserting this in Eq. (2), we find

Table 14–6 Repeatedly Applied Contact Strength [latex]S_{c} ext { at } 10^{7}[/latex] Cycles and 0.99 Reliability for Steel Gears Source: ANSI/AGMA 2001-D04.
Material Designation	Heat Treatment	Minimum Surface [latex] ext { Hardness } 1[/latex]	Allowable Contact Stress [latex] ext { Number, }^{2}{ }^{\prime} S_{c}, ext { psi }[/latex]
Material Designation	Heat Treatment	Minimum Surface [latex] ext { Hardness } 1[/latex]	Grade 1	Grade 2	Grade 3
[latex] ext { Steel }^{3}[/latex]	Through [latex] ext { hardened }{ }^{4}[/latex]	See Fig. 14–5	See Fig. 14–5	See Fig. 14–5	—
	[latex] ext { Flame }^{5}[/latex] or induction	50 HRC	170 000	190 000	—
	[latex] ext { hardened }^{5}[/latex]	54 HRC	175 000	195 000	—
	Carburized and [latex] ext { hardened }^{5}[/latex]	[latex] ext { See Table } 9^{*}[/latex]	180 000	225 000	275 000
	[latex] ext { Nitrided }^{5}[/latex] (through	83.5 HR15N	150 000	163 000	175 000
	hardened steels)	84.5 HR15N	155 000	168 000	180 000
2.5% chrome (no aluminum)	[latex] ext { Nitrided }^{5}[/latex]	87.5 HR15N	155 000	172 000	189 000
Nitralloy 135M	[latex] ext { Nitrided }^{5}[/latex]	90.0 HR15N	170 000	183 000	195 000
Nitralloy N	[latex] ext { Nitrided }^{5}[/latex]	90.0 HR15N	172 000	188 000	205 000
2.5% chrome (no aluminum)	[latex] ext { Nitrided }^{5}[/latex]	90.0 HR15N	176 000	196 000	216 000

Notes: See ANSI/AGMA 2001-D04 for references cited in notes 1–5.

[latex]{ }^{1} ext { Hardness }[/latex] to be equivalent to that at the start of active profile in the center of the face width.

[latex]{ }^{2} ext { See }[/latex] Tables 7 through 10 for major metallurgical factors for each stress grade of steel gears.

[latex]{ }^{3} ext { The }[/latex] steel selected must be compatible with the heat treatment process selected and hardness required.

[latex]{ }^{4} ext { These }[/latex] materials must be annealed or normalized as a minimum.

[latex]{ }^{5} ext { The }[/latex] allowable stress numbers indicated may be used with the case depths prescribed in 16.1.

*Table 9 of ANSI/AGMA 2001-D04 is a comprehensive tabulation of the major metallurgical factors affecting [latex]S_{t} ext { and } S_{c}[/latex] of carburized and hardened steel gears.

[latex](F)_{ ext {wear }}=\left(\frac{2300(0.900)}{170000(1) 0.885} ight)^{2} 2(2502) 1(1.48) 1.14 \frac{1.247(1)}{4.5(0.1286)}=3.44 ext { in }[/latex]

Make face width 3.50 in. Correct [latex]K_{s} ext { and } K_{m}[/latex]:

[latex]K_{s}=1.192\left(\frac{3.50 \sqrt{0.309}}{4} ight)^{0.0535}=1.147[/latex]

[latex]\frac{F}{10 d_{p}}=\frac{3.50}{10(4.5)}=0.0778[/latex]

[latex]C_{p f}=0.0778-0.0375+0.0125(3.50)=0.0841[/latex]

[latex]K_{m}=1+(1)[0.0841(1)+0.175(1)]=1.259[/latex]

The bending stress induced by [latex]W^{t}[/latex] in bending, from Eq. (14–15), is

[latex](\sigma)_{P}=2502(1) 1.48(1.147) \frac{4}{3.50} \frac{1.259(1)}{0.32}=19100 psi[/latex]

The AGMA factor of safety in bending of the pinion, from Eq. (14–41), is

[latex]S_{F}=\frac{S_{t} Y_{N} /\left(K_{T} K_{R} ight)}{\sigma}=\frac{ ext { fully corrected bending strength }}{ ext { bending stress }}[/latex] (14–41)

[latex]\left(S_{F} ight)_{P}=\frac{40310(0.938) /[1(0.885)]}{19100}=2.24[/latex]

Gear tooth bending. Use cast gear blank because of the 18-in pitch diameter. Use the same material, heat treatment, and nitriding. The load-induced bending stress is in the ratio of [latex]J_{P} / J_{G}[/latex]. Then

[latex](\sigma)_{G}=19100 \frac{0.32}{0.415}=14730 psi[/latex]

The factor of safety of the gear in bending is

[latex]\left(S_{F} ight)_{G}=\frac{40310(0.961) /[1(0.885)]}{14730}=2.97[/latex]

Pinion tooth wear. The contact stress, given by Eq. (14–16), is

[latex]\left(\sigma_{c} ight)_{P}=2300\left[2502(1) 1.48(1.147) \frac{1.259}{4.5(3.5)} \frac{1}{0.129} ight]^{1 / 2}=118000 psi[/latex]

The factor of safety from Eq. (14–42), is

[latex]S_{H}=\frac{S_{c} Z_{N} C_{H} /\left(K_{T} K_{R} ight)}{\sigma_{c}}=\frac{ ext { fully corrected contact strength }}{ ext { contact stress }}[/latex] (14–42)

[latex]\left(S_{H} ight)_{P}=\frac{170000(0.900) /[1(0.885)]}{118000}=1.465[/latex]

By our definition of factor of safety, pinion bending is [latex]\left(S_{F} ight)_{P}=2.24[/latex], and wear is [latex]\left(S_{H} ight)_{P}^{2}=(1.465)^{2}=2.15[/latex].

Gear tooth wear. The hardness of the gear and pinion are the same. Thus, from Fig. 14–12, [latex]C_{H}=1[/latex], the contact stress on the gear is the same as the pinion, [latex]\left(\sigma_{c} ight)_{G}=[/latex] 118 000 psi. The wear strength is also the same, [latex]S_{c}=170000[/latex] psi. The factor of safety of the gear in wear is

[latex]\left(S_{H} ight)_{G}=\frac{170000(0.929) /[1(0.885)]}{118000}=1.51[/latex]

So, for the gear in bending, [latex]\left(S_{F} ight)_{G}=2.97[/latex], and wear [latex]\left(S_{H} ight)_{G}^{2}=(1.51)^{2}=2.29[/latex].

Rim. Keep [latex]m_{B} \geq 1.2[/latex]. The whole depth is [latex]h_{t}= ext { addendum }+ ext { dedendum }=1 / P_{d}+[/latex] [latex]1.25 / P_{d}=2.25 / \bar{P}_{d}=2.25 / 4=0.5625[/latex] in. The rim thickness [latex]t_{R}[/latex] is

[latex]t_{R} \geq m_{B} h_{t}=1.2(0.5625)=0.675 ext { in }[/latex]

In the design of the gear blank, be sure the rim thickness exceeds 0.675 in; if it does not, review and modify this mesh design.

Question 14.8: Design a 4:1 spur-gear reduction for a 100-hp, three-phase s...

This Question has been Answered.

Already have an account?

Login

Related Answered Questions