Design a plain surface journal bearing to carry a steady radial load of 1500 lb while the shaft rotates at 850 rpm. The shaft stress analysis determines that the minimum acceptable diameter at the journal is 2.10 in. The shaft is part of a machine requiring good precision.

Question

Accepted Answer

Step 1. Let’s select [latex]D = 2.50[/latex] in. Then [latex]R = 1.25[/latex] in.
Step 2. For [latex]p = 200[/latex] psi, [latex]L[/latex] must be
[latex]L = F/pD = 1500/(200)(2.50) = 3.00[/latex] in
For this value of [latex]L, L/D = 3.00/2.50 = 1.20[/latex]. In order to use one of the standard design charts, let’s change [latex]L[/latex] to 2.50 in so that [latex]L/D = 1.0[/latex]. This is not essential, but it eliminates interpolation. The actual pressure is then

[latex]p = F/LD = 1500/(2.50)(2.50) = 240[/latex] psi

This is an acceptable pressure.
Step 3. From Figure 16–4, [latex]C_d = 0.003[/latex] in is suitable for the diametral clearance, based on [latex]D = 2.50[/latex] in and [latex]n = 850[/latex] rpm, and [latex]C_r = C_d/2 = 0.0015[/latex] in. Also,

[latex]R/C_r = 1.25/0.0015 = 833[/latex]
This value is used in later calculations.

Step 4. For the precision desired in this machine, use a surface finish of 16 to 32 min, requiring a ground journal.
Step 5. Minimum film thickness (design value):
[latex]h_o = 0.00025D = 0.00025(2.50) = 0.0006[/latex] in (approx.)
Step 6. Film thickness variable:
[latex]h_o/C_r = 0.0006/0.0015 = 0.40[/latex]
Step 7. From Figure 16–8, for [latex]h_o/C_r = 0.40[/latex] and [latex]L/D = 1[/latex], we can read [latex]S = 0.13[/latex].
Step 8. Rotational speed in revolutions per second:
[latex]n_s = n/60 = 850/60 = 14.2[/latex] rev/s

Step 9. Solve for the viscosity from the Sommerfeld number, [latex]S[/latex]:

[latex]\mu=\frac{SP}{n_s(R/C_R)^2}=\frac{(0.13)(240)}{(14.2)(833)^2}= 3.17 × 10^{-6}[/latex] reyn

Step 10. From the viscosity chart, Figure 16–7, SAE 30 oil is required to ensure a sufficient viscosity at 160°F. The actual expected viscosity of SAE 30 at 160°F is approximately [latex]3.3 × 10^{-6}[/latex] reyn.
Step 11. For the actual viscosity, the Sommerfeld number would be

[latex]S=\frac{\mu n_s(R/C_r)^2}{P}=\frac{(3.3 × 10^{-6})(14.2)(833)^2}{42}=0.135[/latex]

Step 12. Coefficient of friction variable (from Figure 16–9): [latex]f(R/C_r) = 3.5[/latex] for [latex]S = 0.135[/latex] and [latex]L/D = 1[/latex].

Now, because [latex]R/C_r = 833[/latex],
[latex]f = 3.5/833 = 0.0042[/latex]
Step 13. Friction torque:
[latex]T_f = fFR = (0.0042)(1500)(1.25) = 7.88[/latex] lb . in

Step 14. Frictional power:
[latex]P_f = T_fn/63 000 = (7.88)(850)/63 000 =0.106[/latex] hp

Comment: A qualitative evaluation of the result would require more knowledge about the application. But note that a coefficient of friction of 0.0042 is quite low. It is likely that a machine requiring such a large shaft and with such high bearing forces also requires a large power to drive it. Then the 0.106-hp friction power would appear small.
Thermal considerations are also important to determine how much energy must be dissipated from the bearing. Converting the frictional power loss to thermal power gives

[latex]P_f=0.106hp\frac{745.7W}{hp}=79.0W[/latex]

Expressing this in U.S. Customary units gives

[latex]P_f=79.0W\frac{1 Btu/h}{0.293 W}= 270 Btu/h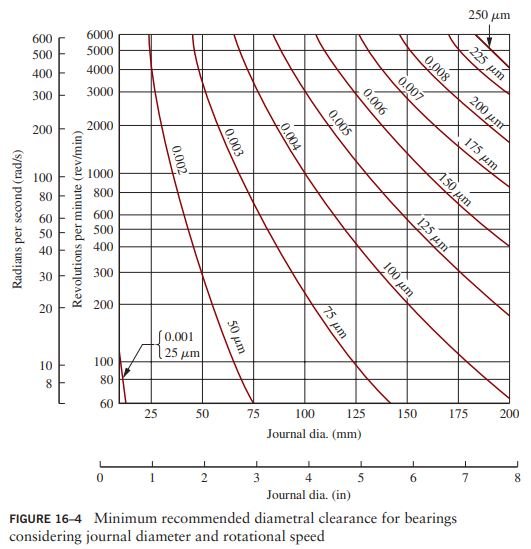[/latex]

Question 16.4: Design a plain surface journal bearing to carry a steady rad...

This Question has been Answered.

Already have an account?

Login

Related Answered Questions