Only the thermal design will be considered.
This example illustrates Kern’s method.
Coolant is corrosive, so assign to tube-side.
Heat capacity methanol =2.84kJ/kg∘C
Heat load =3600100,000×2.84(95−40)=4340kW
Heat capacity water =4.2kJ/kg∘C
Cooling water flow =4.2(40−25)4340=68.9kg/s
ΔTlm=ln(40−25)(95−40)(95−40)−(40−25)=31∘C (12.4)
Use one shell pass and two tube passes
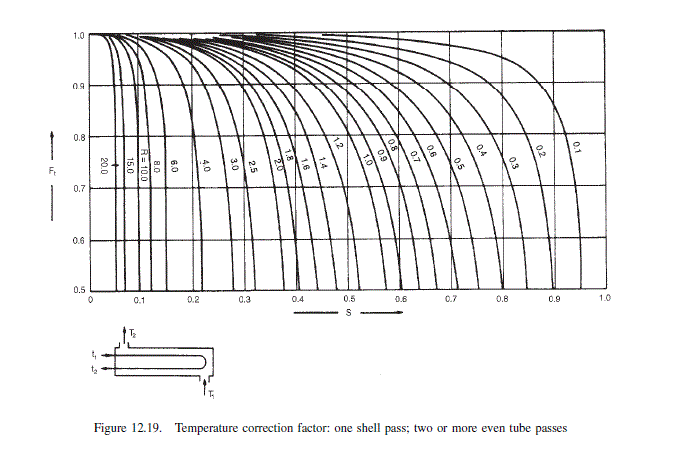
R=40−2595−40=3.67 (12.6)
S=95−2540−25=0.21 (12.7)
From Figure 12.19
Ft=0.85
ΔTm=0.85×31=26∘C
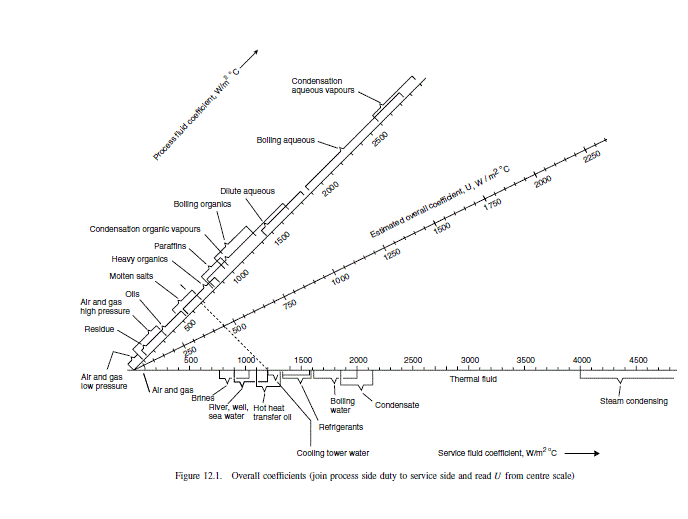
From Figure 12.1
U=600W/m2∘C
Provisional area
A=26×6004340×103=278m2 (12.1)
Choose 20 mm o.d., 16 mm i.d., 4.88-m-long tubes (43in.×16ft), cupro-nickel.
Allowing for tube-sheet thickness, take
L = 4.83 m
Area of one tube =4.83×20×10−3π=0.303m2
Number of tubes =0.303278=918
As the shell-side fluid is relatively clean use 1.25 triangular pitch.
Bundle diameter Db=20(0.249918)1/2.207=826mm (12.3b)
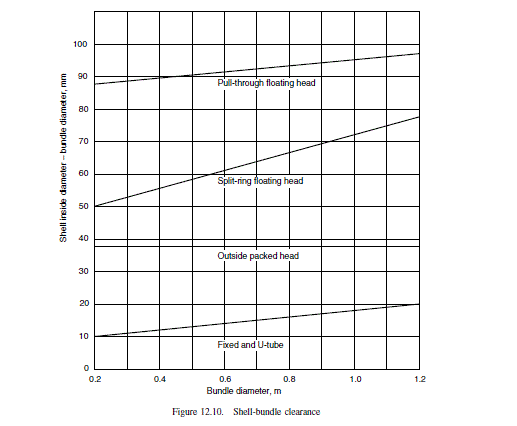
Use a split-ring floating head type.
From Figure 12.10, bundle diametrical clearance = 68 mm,
shell diameter, Ds=826+68=894mm
(Note. nearest standard pipe sizes are 863.6 or 914.4 mm).
Shell size could be read from standard tube count tables.
Tube-side coefficient
Mean water temperature =240+25=33∘C
Tube cross-sectional area =4π×162=201mm2
Tubes per pass =2918=459
Total flow area =459×201×10−6=0.092m2
Water mass velocity =0.09268.9=749kg/sm2
Density water =995kg/m3
Water linear velocity =995749=0.75m/s
hi=160.24200(1.35+0.02×33)0.750.8=3852W/m2∘C (12.17)
The coefficient can also be calculated using equation 12.15; this is done to illustrate use of this method.
kfhidi=jhRePrr0.33(μwμ)0.14 (12.15)
kfhidi=jhRePr0.33(μwμ)0.14
Viscosity of water =0.8mNs/m2
Thermal conductivity =0.59W/m∘C
Re=μρudi=0.8×10−3995×0.75×16×10−3=14,925
Pr=kfCpμ=0.594.2×103×0.8×10−3=5.7
Neglect (μwμ)
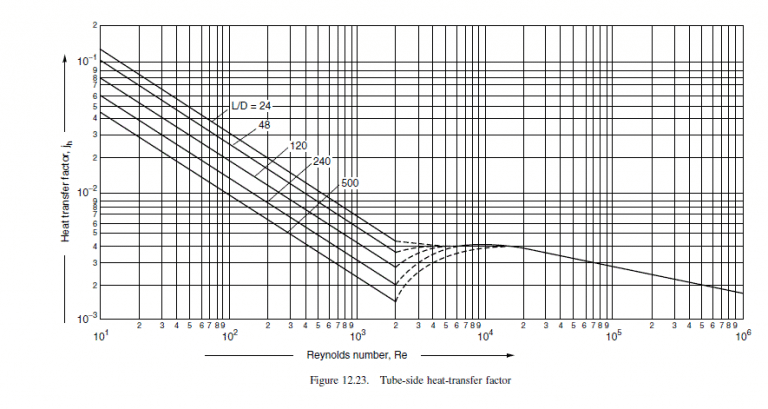
diL=164.83×103=302
From Figure 12.23,jh=3.9×10−3
hi=16×10−30.59×3.9×10−3×14,925×5.70.33=3812W/m2∘C
Checks reasonably well with value calculated from equation 12.17; use lower figure.
Shell-side coefficient
Choose baffle spacing =5Ds=5894=178mm
Tube pitch =1.25×20=25mm
Cross-flow area As=25(25−20)894×178×10−6=0.032m2 (12.21)
Mass velocity, GS=3600100,000×0.0321=868kg/sm2
Equivalent diameter de=201.1(252−0.917×202)=14.4mm (12.23)
Mean shell side temperature =295+40=68∘C
Methanol density =750kg/m3
Viscosity =0.34mNs/m2
Heat capacity =2.84kJ/kg∘C
Thermal conductivity =0.19W/m∘C
Re=μGsde=0.34×10−3868×14.4×10−3=36,762 (12.24)
Pr=kfCpμ=0.192.84×103×0.34×10−3=5.1
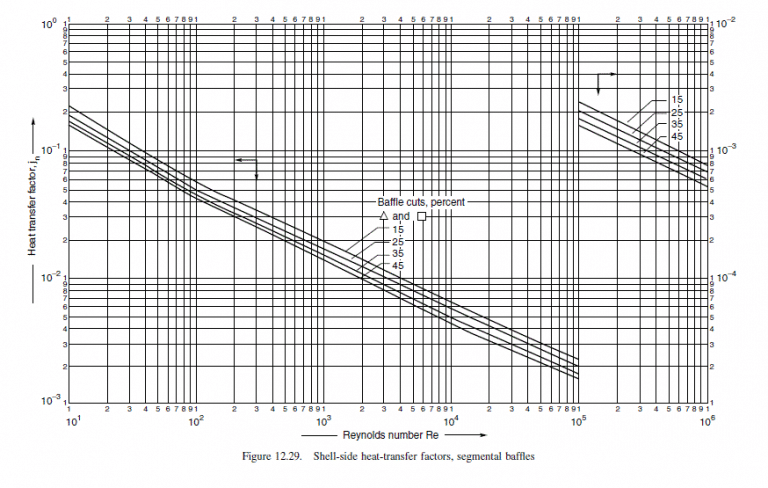
Choose 25 per cent baffle cut, from Figure 12.29
jh=3.3×10−3
Without the viscosity correction term
hs=14.4×10−30.19×3.3×10−3×36,762×5.11/3=2740W/m2∘C
Estimate wall temperature
Mean temperature difference =68−33=35∘C
across all resistances
across methanol film =hoU×ΔT=2740600×35=8∘C
Mean wall temperature =68−8=60∘C
μw=0.37mNs/m2
(μwμ)0.14=0.99
which shows that the correction for a low-viscosity fluid is not significant.
Overall coefficient
Thermal conductivity of cupro-nickel alloys D 50 W/m∘C.
Take the fouling coefficients from Table 12.2; methanol (light organic) 5000Wm−2∘C−1,
brackish water (sea water), take as highest value, 3000 Wm−2∘C−1
| Fluid |
Coefficient (W/m2∘C) |
Factor (resistance) (m2°C/W) |
| River water |
3000−12,000 |
0.0003−0.0001 |
| Sea water |
1000−3000 |
0.001−0.0003 |
| Cooling water (towers) |
3000−6000 |
0.0003−0.00017 |
| Towns water (soft) |
3000−5000 |
0.0003−0.0002 |
| Towns water (hard) |
1000−2000 |
0.001−0.0005 |
| Steam condensate |
1500−5000 |
0.00067−0.0002 |
| Steam (oil free) |
4000−10,000 |
0.0025−0.0001 |
| Steam (oil traces) |
2000−5000 |
0.0005−0.0002 |
| Refrigerated brine |
3000−5000 |
0.0003−0.0002 |
| Air and industrial gases |
5000−10,000 |
0.0002−0.0001 |
| Flue gases |
2000−5000 |
0.0005−0.0002 |
| Organic vapours |
5000 |
0.0002 |
| Organic liquids |
5000 |
0.0002 |
| Light hydrocarbons |
5000 |
0.0002 |
| Heavy hydrocarbons |
2000 |
0.0005 |
| Boiling organics |
2500 |
0.0004 |
| Condensing organics |
5000 |
0.0002 |
| Heat transfer fluids |
5000 |
0.0002 |
| Aqueous salt solutions |
3000−5000 |
0.0003−0.0002 |
Uo1=27401+50001+2×5020×10−3ln(1620) +1620×30001+1620×38121 Uo=738W/m2∘C (12.2)
well above assumed value of 600W/m2∘C.
Pressure drop
Tube-side
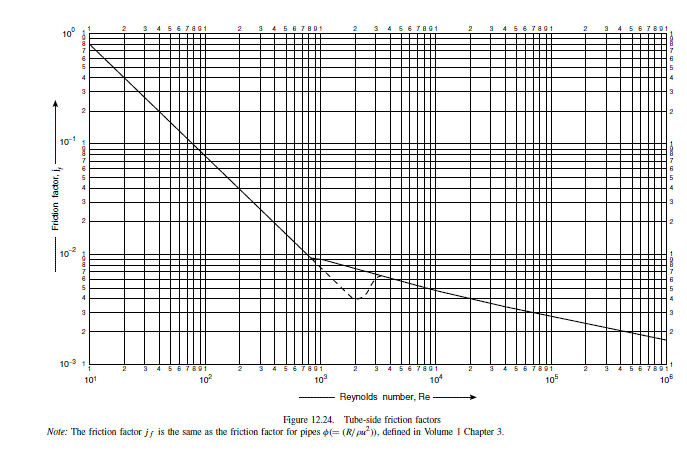
From Figure 12.24, for Re=14,925
jf=4.3×10−3
Neglecting the viscosity correction term
ΔPt=2(8×4.3×10−3(164.83×103)+2.5)2995×0.752 =7211N/m2=7.2kPa(1.1psi) (12.20)
low, could consider increasing the number of tube passes.
Shell side
Linear velocity =ρGs=750868=1.16m/s
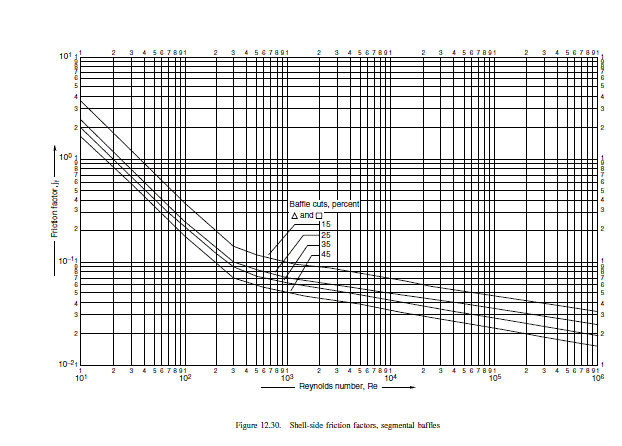
From Figure 12.30, at Re=36,762
jf=4×10−2
Neglect viscosity correction
ΔPs=8×4×10−2(14.4894)(1784.83×103)2750×1.162 (12.26)
=272,019N/m2=272kPa(39psi) too high,
could be reduced by increasing the baffle pitch. Doubling the pitch halves the shell-side velocity, which reduces the pressure drop by a factor of approximately (1/2)2
ΔPs=4272=68kPa(10psi), acceptable
This will reduce the shell-side heat-transfer coefficient by a factor of (1/2)0.8(ho∝ Re0.8∝us0.8)
ho=2740×(21)0.8=1573W/m2∘C
This gives an overall coefficient of 615 W/m2∘C− still above assumed value of 600 W/m2∘C.