Design of a Batch Reactor
Ethyl acetate is to be produced in a batch reactor operating at 100ºC and at 37.2 percent conversion of acetic acid. If the reactor charge of the preceding example is used and 20 minutes are needed to discharge, clean, and charge the reactor, what size reactor is required to produce, on average, 1250 kg of the ester per hour? What heat program should be followed to ensure the reactor remains at 100ºC? Data: See the preceding illustration.
The starting point here is Eq. 14.1-13, which, for the present case, can be written
\frac{d C_{ i }}{d t}=\sum_{ j =1}^{ M } \nu_{ ij } r_{ j } (14.1-13)
\frac{d C_{ EA }}{d t}=k C_{ A } C_{ E }-k^{\prime} C_{ EA } C_{ W } (a)
where, at any extent of reaction \hat{X}=X / V \text {, we have }
| Initial Concentration | Concentration* at the Extent of Reaction \hat{X} | |
| Acetic acid | 4.17 kmol / m ^{3} | 4.17-\hat{X} kmol / m ^{3} |
| Ethanol | 10.9 | 10.9-\hat{X} |
| Ethyl acetate | 0 | \hat{X} |
| Water | 16.1 | 16.1+\hat{X} |
| *Note that \hat{X}= X/V is the molar extent of reaction per unit volume and has units of concentration. | ||
Thus, Eq. a becomes
\begin{aligned}r \equiv \frac{d \hat{X}}{d t} &=k(4.17-\hat{X})(10.9-\hat{X})-k^{\prime}(16.1+\hat{X}) \hat{X} \\&=4.76 \times 10^{-4}(4.17-\hat{X})(10.9-\hat{X})-1.63 \times 10^{-4}(16.1+\hat{X}) \hat{X} \\&=2.163 \times 10^{-2}\left(1-0.4528 \hat{X}-0.01447 \hat{X}^{2}\right) kmol /\left( m ^{3} min \right)\end{aligned} (b)
which can be rearranged to
2.163 \times 10^{-2} d t=\frac{d \hat{X}}{1-0.4528 \hat{X}+0.01447 \hat{X}^{2}}
Integrating this equation between t = 0 and the time t \text { yields }{ }^{2}
2.163 \times 10^{-2} \int_{0}^{t} d t=2.163 \times 10^{-2} \frac{ kmol }{ m ^{3} \min } \times t=\int_{0}^{\hat{X}} \frac{d \hat{X}}{1-0.4528 \hat{X}+0.01447 \hat{X}^{2}}
or
\ln \left\{\frac{0.02894 \hat{X}-0.8364}{0.02894 \hat{X}-0.0692}\right\}-\ln \left(\frac{0.8364}{0.0692}\right)=0.8297 \times 10^{-2} t (c)
and for \hat{X} = 1.55 (37.2 percent conversion of the acid) we have 0.8297 × 10−2t = 0.9896 min or t = 119.3 min.
Thus, the total cycle time for the batch reactor is 119.3+20 = 139.3 min = 2.322 hr. Therefore, 2.322 hr × 1250 kg/hr = 2902.5 kg of ester that must be produced in each reactor cycle. Since, in this example, the conversion and feed in the batch reactor are the same as those in the previous illustration, the effluent concentration of the ester is again
C_{ EA }=1.55 kmol m 3=136.4 kg / m ^{3}
Therefore, the reactor volume is
V=\frac{2902.5 kg }{136.4 kg / m ^{3}}=21.28 m ^{3}
{ }^{2} \text { Note that } \int \frac{d X}{a+b X+c X^{2}}=\frac{1}{\sqrt{2}} \ln \left[\frac{2 c X+b-\sqrt{-q}}{2 c X+b+\sqrt{-q}}\right] \quad \text { where } q=4 a c-b^{2}
To compute the reactor heat program, that is, the heating rate as a function of time to keep the reactor at constant temperature, Eq. 14.1-16 is used, noting that for the isothermal case dT/dt = 0, so that
\dot{Q}=V\left(\Delta_{ rxn } H\right) \cdot r (d)
where r is given by Eq. b and \hat{X} is given as a function of time by Eq. c.
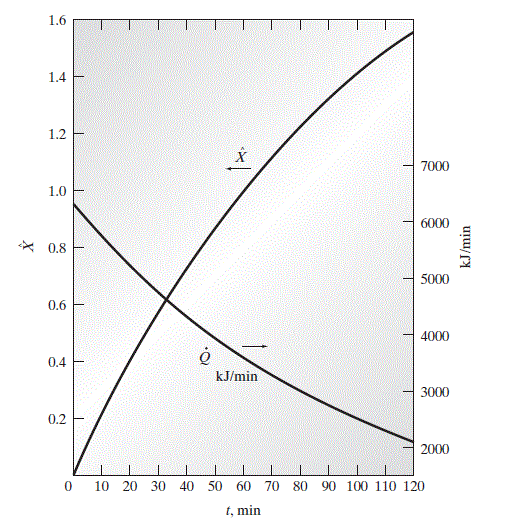
The instantaneous values of X \text { and } \dot{Q} as a function of time are plotted in the following figure.
The heat flow rate \dot{Q} and extent of reaction \hat{X} for ethyl acetate production in a batch reactor.
