Question 4.5: Determine the bending moment at the point B in the simply su...

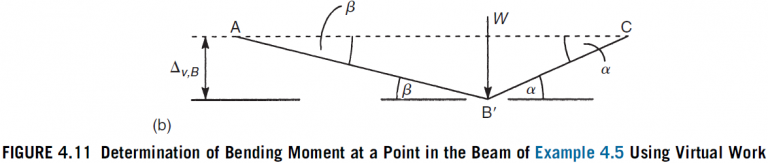
We determined the support reactions for this particular beam in Example 4.4. In this example, however, we are interested in the actual internal moment, M_{ B }, at the point of application of the load. We must therefore impose a virtual displacement that relates the internal moment at B to the applied load and excludes other unknown external forces, such as the support reactions, and unknown internal force systems, such as the bending moment distribution along the length of the beam. Therefore, if we imagine that the beam is hinged at B and that the lengths AB and BC are rigid, a virtual displacement, \Delta_{v, B }, at B results in the displaced shape shown in Fig. 4.11(b). Note that the support reactions at A and C do no work and that the internal moments in AB and BC do no work because AB and BC are rigid links. From Fig. 4.11(b),

\Delta_{v, B }=a \beta=b \alpha  (i)

Hence,

and the angle of rotation of BC relative to AB is then

\theta_{ B }=\beta+\alpha=\beta\left(1+\frac{a}{b}\right)=\frac{L}{b} \beta  (ii)

Now, equating the external virtual work done by W to the internal virtual work done by M_{ B } (see Eq. (4.23)), we have

W_{e}=W_{i}  (4.23)

W \Delta_{v, B }=M_{ B } \theta_{ B }  (iii)

Substituting in Eq. (iii) for \Delta_{V, B } from Eq. (i) and for \theta_{ B } from Eq. (ii), we have

which gives

which is the result we would have obtained by calculating the moment of R_{ C }(=W a / L from Example 4.4) about B.