Determine the pinch temperatures and the minimum utility requirements for the streams set out in the table below, for a minimum temperature difference between the streams of 20^{\circ} C. Devise a heat exchanger network to achieve the maximum energy recovery.
| Stream number | Type | Heat capacity kW /{ }^{\circ} C | Source \text { temp. }{ }^{\circ} C | Target \text { temp. }{ }^{\circ} C |
| 1 | hot | 40.0 | 180 | 40 |
| 2 | hot | 30.0 | 150 | 60 |
| 3 | cold | 60.0 | 30 | 180 |
| 4 | cold | 20.0 | 80 | 160 |
The construction of the problem table to find the minimum utility requirement and the pinch temperature is facilitated by using a spreadsheet. The calculations in each cell are repetitive and the formula can be copied from cell to cell using the cell copy commands.
The spreadsheet AS-EASY-AS (TRIUS Inc) was used to develop the tables for this problem.
First calculate the interval temperatures, for \Delta T_{\min }=20^{\circ} C
hot streams T_{\text {int }}=T_{\text {act }}-10^{\circ} C
cold streams T_{ int }=T_{ act }+10^{\circ} C
| Stream | Actual temp. { }^{\circ} C | Interval temp. { }^{\circ} C | ||
| Source | Target | Source | Target | |
| 1 | 180 | 40 | 170 | 30 |
| 2 | 150 | 60 | 140 | 50 |
| 3 | 30 | 180 | 40 | 190 |
| 4 | 80 | 160 | 90 | (170) |
Next rank the interval temperatures, ignoring any duplicated values. Show which streams occur in each interval to aid in the calculation of the combined stream heat capacities:
Now set out the problem table:
| Interval | Interval \text { temp. }{ }^{\circ} C | \Delta T { }^{\circ} C | \begin{array}{c}\Sigma C P_{ c } \times \Sigma C P_{ h } \\kW /{ }^{\circ} C\end{array} | \Delta H KW | Cascade | |
| 190 | 0 | 2900 | ||||
| 1 | 170 | 20 | 60 | 1200 | -1200 | 1700 |
| 2 | 140 | 30 | 40 | 1200 | -2400 | 500 |
| 3 | 90 | 50 | 10 | 500 | -2900 | 0 |
| 4 | 50 | 40 | -10 | -400 | -2500 | 400 |
| 5 | 40 | 10 | 20 | 200 | -2700 | 200 |
| 6 | 30 | 10 | -40 | -400 | -2300 | 600 |
In the last column 2900 kW of heat have been added to eliminate the negative values in the previous column.
So, the hot utility requirement is 2900 kW and the cold, the bottom value in the column, is 600 kW.
The pinch occurs where the heat transferred is zero, that is at interval number 3,90^{\circ} C.
So at the pinch hot streams will be at:
90+10=100^{\circ} C
and the cold at:
90-10=80^{\circ} C
To design the network for maximum energy recovery: start at the pinch and match streams following the rules on stream heat capacities for matches adjacent to the pinch.
Where a match is made: transfer the maximum amount of heat.
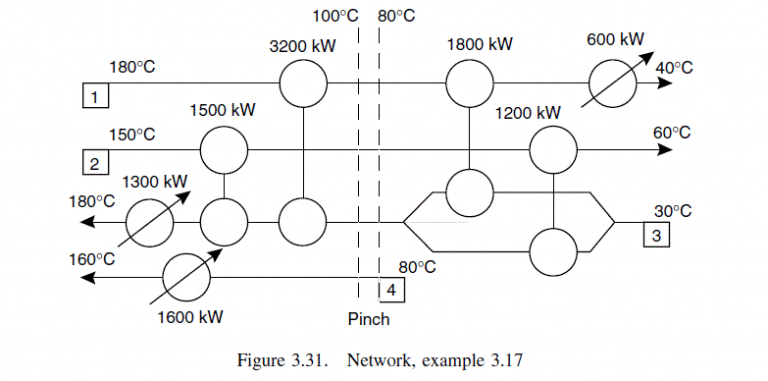
The proposed network is shown in Figure 3.31.
The methodology followed in devising this network was:
Above pinch
\text { 1. } C P_{\text {hot }} \leq C P_{\text {cold }}
2. Can match stream 1 and 2 with stream 3 but not with stream 4.
3. Check the heat available in bringing the hot streams to the pinch temperature.
stream 1 \Delta H=40.0(180-100)=3200 kW
stream 2 \Delta H=30.0(150-100)=1500 kW
4. Check the heat required to bring the cold streams from the pinch temperature to their target temperatures.
stream 3 \Delta H=60.0(180-80)=6000 kW
stream 4 \Delta H=20.0(160-80)=1600 kW
5. Match stream 1 with 3 and transfer 3200 kW, that satisfies (ticks off) stream 1.
6. Match stream 2 with 3 and transfer 1500 kW, that ticks off stream 2.
7. Include a heater on stream 3 to provide the balance of the heat required:
\Delta H_{\text {hot }}=6000-4700=1300 kW
8. Include a heater on stream 4 to provide heat load required, 1600 kW.
Below pinch
\text { 9. } C P_{ hot } \geq C P_{\text {cold }}
10. Note that stream 4 starts at the pinch temperature so can not provide any cooling below the pinch.
11. Cannot match stream 1 or 2 with stream 3 at the pinch.
12. So, split stream 3 to reduce CP. An even split will allow both streams 1 and 2 to be matched with the split streams adjacent to the pinch, so try this:
13. Check the heat available from bringing the hot streams from the pinch temperature to their target temperatures.
stream 1 \Delta H=40.0(100-40)=2400 kW
stream 2 \Delta H=30.0(100-60)=1200 kW
14. Check the heat required to bring the cold streams from their source temperatures to the pinch temperature:
stream 3 \Delta H=60.0(80-30)=3000 kW
stream 4 is at the pinch temperature.
15. Note that stream 1 can not be brought to its target temperature of 40^{\circ} C by full interchange with stream 3 as the source temperature of stream 3 is 30^{\circ} C, so \Delta T_{\min } would be violated. So transfer 1800 kW to one leg of the split stream 3.
16. Check temperature at exit of this exchanger:
\text { Temp out }=100-\frac{1800}{40}=55^{\circ} C , \text { satisfactory }
17. Provide cooler on stream 1 to bring it to its target temperature, cooling needed:
\Delta H_{\text {cold }}=2400-1800=600 kW
18. Transfer the full heat load from stream 2 to second leg of stream 3; this satisfies both streams.
Note that the heating and cooling loads, 2900 kW and 600 kW, respectively, match those predicted from the problem table.
