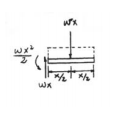
Determine the variation in the width b as a function of x for the cantilevered beam that supports a uniform distributed load along its centerline so that it has the same maximum bending stress \sigma_{\text {allow }} throughout its length. The beam has a constant depth t.
Section Properties:
I=\frac{1}{12} b t^{3} \quad S=\frac{I}{c}=\frac{\frac{1}{12} b t^{3}}{\frac{t}{2}}=\frac{t^{2}}{6} bBending Stress:
\sigma_{\text {allow }}=\frac{M}{S}=\frac{\frac{w x^{2}}{2}}{\frac{2}{6} b}=\frac{3 w x^{2}}{t^{2} b}\quad(1)At x = L , b = b_{0}
\sigma_{\text {allow }}=\frac{3 w L^{2}}{t^{2} b_{0}}\quad(2)Equating Eqs. (1) and (2) yields:
\frac{3 w x^{2}}{r^{2} b}=\frac{3 w L^{2}}{t^{2} b_{0}}b=\frac{b_{0}}{L^{2}} x^{2}
