Question 15.4: Effect of Inert Gases on Equilibrium Composition A mixture o...

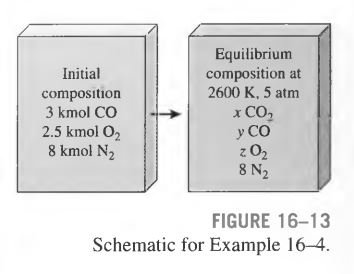
A gas mixture is heated to a high temperature. The equilibrium composition at the specified temperature is to be determined.

Assumptions 1 The equilibrium composition consists of \mathrm{CO}_{2}, CO, \mathrm{O}_{2}, and \mathrm{N}_{2}. 2 The constituents of the mixture are ideal gases.

Analysis This problem is similar to Example 16-3, except that it involves an inert gas \mathrm{N}_{2}. At 2600 K, some possible reactions are \mathrm{O}_{2} \rightleftharpoons 2O (In K_{p}= -7.521), \mathrm{N}_{2} \rightleftharpoons 2 \mathrm{~N}\left(\ln K_{p}=-28.304\right), \frac{1}{2} \mathrm{O}_{2}+\frac{1}{2} \mathrm{~N}_{2} \rightleftharpoons \mathrm{NO}\left(\right. In K_{p}=-2.671), and \mathrm{CO}+\frac{1}{2} \mathrm{O}_{2} \rightleftharpoons \mathrm{CO}_{2} (In K_{p}=2.801 or K_{p}=16.461 ). Based on these K_{p} values, we conclude that the \mathrm{O}_{2} and \mathrm{N}_{2} will not dissociate to any appreciable degree, but a small amount will combine to form some oxides of nitrogen. (We disregard the oxides of nitrogen in this example, but they should be considered in a more refined analysis.) We also conclude that most of the \mathrm{CO} will combine with \mathrm{O}_{2} to form \mathrm{CO}_{2}. Notice that despite the changes in pressure, the number of moles of CO and \mathrm{O}_{2} and the presence of an inert gas, the K_{p} value of the reaction is the same as that used in Example 16-3.

The stoichiometric and actual reactions in this case are

Stoichiometric:          \left.\mathrm{CO}+\frac{1}{2} \mathrm{O}_{2} \rightleftharpoons \mathrm{CO}_{2} \text { (thus } \nu_{\mathrm{CO}_{2}}=1, \nu_{\mathrm{CO}}=1, \text { and } \nu_{\mathrm{O}_{2}}=\frac{1}{2}\right)

Actual:      3 \mathrm{CO}+2.5 \mathrm{O}_{2}+8 \mathrm{~N}_{2} \longrightarrow \underbrace{x \mathrm{CO}_{2}}_{\text {products }}+\underbrace{y \mathrm{CO}+z \mathrm{O}_{2}}_{\begin{array}{l}\text { reactants } \\\text { (leftover) }\end{array}}+\underbrace{8 \mathrm{~N}_{2}}_{\text {inert }}

C balance:                  3 = x + y     or     y = 3 — x

O balance:         8 = 2x + y + 2z     or          z=2.5-\frac{x}{2}

Total number of moles:        N_{\text {total }}=x+y+z+8=13.5-\frac{x}{2}

Assuming ideal-gas behavior for all components, the equilibrium constant relation (Eq. 16-15) becomes

Substituting, we get

Solving for x yields

x=2.754

Then

y=3 – x=0.246

Therefore, the equilibrium composition of the mixture at 2600 K and 5 atm is

Discussion Note that the inert gases do not affect the K_{p} value or the K_{p} relation for a reaction, but they do affect the equilibrium composition.