Engine oil is cooled by flowing through a tube at a rate of \dot{M}_{f} = 0.05 kg/s with an inlet temperature \left\langle T_{f}\right\rangle _{0}= 80^{\circ }C. The surface of the tube is cooled and maintained at a constant temperature of T_{s} = 30^{\circ }C (by, e.g., removing the heat from this surface to another fluid). This is rendered in Figure (a).
The tube has a diameter D = 2 cm, and a length L = 20 m (this can be a coiled tube instead of a straight tube). The Nusselt number is \left\langle Nu\right\rangle _{D}= 3.66.
(a) Draw the thermal circuit diagram and show the expected fluid temperature distribution.
(b) Determine the number of transfer units NTU.
(c) Determine the effectiveness \epsilon _{he}.
(d) Determine the fluid exit temperature \left\langle T_{f}\right\rangle _{L}.
(e) Determine the average convection resistance \left\langle R_{u}\right\rangle _{L}.
(f) Determine the average convection heat transfer rate \left\langle Q_{u}\right\rangle _{L-0}.
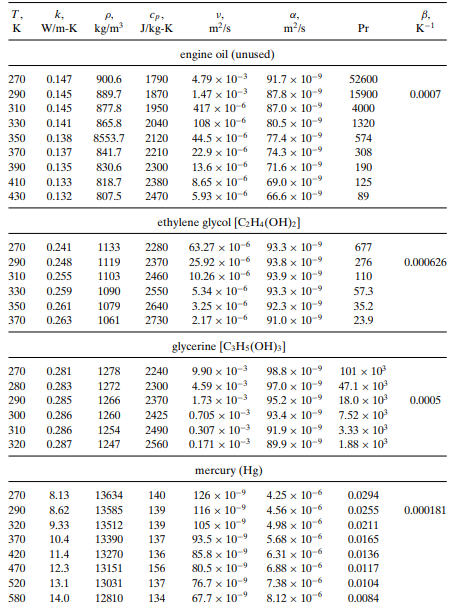
Evaluate the oil thermophysical properties from Table and at T = 330 K.