Estimate the horsepower rating of the gear in the previous example based on obtaining an infinite life in bending.
Question 14.2: Estimate the horsepower rating of the gear in the previous e...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
The rotating-beam endurance limit is estimated from Eq. (6–8)
S_{e}^{\prime}=\left\{\begin{array}{ll}0.5 S_{u t} & S_{u t} \leq 200 kpsi (1400 MPa ) \\100 kpsi & S_{u t}>200 kpsi \\700 MPa & S_{u t}>1400 MPa\end{array}\right. (6–8)
S_{e}^{\prime}=0.5 S_{u t}=0.5(55)=27.5 kpsi
To obtain the surface finish Marin factor k_{a} we refer to Table 6–3 for machined surface, finding a = 2.70 and b = −0.265. Then Eq. (6–19) gives the surface finish Marin factor k_{a} as
k_{a}=a S_{u t}^{b} (6–19)
k_{a}=a S_{u t}^{b}=2.70(55)^{-0.265}=0.934
| Table 6–3 A_{0.95 \sigma} Areas of Common Nonrotating Structural Shapes | |
 |
\begin{aligned}A_{0.95 \sigma} &=0.01046 d^{2} \\d_{e} &=0.370 d\end{aligned} |
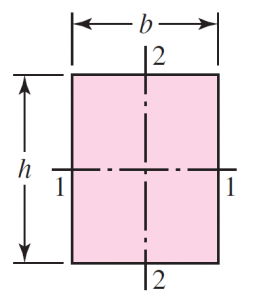 |
\begin{aligned}A_{0.95 \sigma} &=0.05 h b \\d_{e} &=0.808 \sqrt{h b}\end{aligned} |
 |
A_{0.95 \sigma}=\left\{\begin{array}{ll}0.10 at_{f} & &\text { axis } 1-1 \\0.05ba & t_{f}>0.025a&\text { axis } 2-2\end{array}\right. |
 |
A_{0.95 \sigma}=\left\{\begin{array}{ll}0.05 a b & \text { axis } 1-1 \\0.052 x a+0.1 t_{f}(b-x) & \text { axis } 2-2\end{array}\right. |
The next step is to estimate the size factor k_{b}. From Table 13–1, the sum of the addendum and dedendum is
| Table 13–1 Standard and Commonly Used Tooth Systems for Spur Gears | |||
| Tooth System | Pressure Angle \phi, deg | Addendum a | Dedendum b |
| Full depth | 20 | 1 / P_{d} \text { or } 1 m | 1.25 / P_{d} \text { or } 1.25 m |
| 1.35 / P_{d} \text { or } 1.35 m | |||
| 22 \frac{1}{2} | 1 / P_{d} \text { or } 1 m | 1.25 / P_{d} \text { or } 1.25 m | |
| 1.35 / P_{d} \text { or } 1.35 m | |||
| 25 | 1 / P_{d} \text { or } 1 m | 1.25 / P_{d} \text { or } 1.25 m | |
| 1.35 / P_{d} \text { or } 1.35 m | |||
| Stub | 20 | 0.8 / P_{d} \text { or } 0.8 m | 1 / P_{d} \quad \text { or } 1 m |
l=\frac{1}{P}+\frac{1.25}{P}=\frac{1}{8}+\frac{1.25}{8}=0.281 \text { in }
The tooth thickness t in Fig. 14–1b is given in Sec. 14–1 [Eq. (b)] as t=(4 l x)^{1 / 2} when x = 3Y/(2P) from Eq. (14–3). Therefore, since from Ex. 14–1 Y = 0.296 and P = 8,
\frac{t / 2}{x}=\frac{l}{t / 2} \quad \text { or } \quad x=\frac{t^{2}}{4 l} (b)
Y=\frac{2 x P}{3} (14–3)
x=\frac{3 Y}{2 P}=\frac{3(0.296)}{2(8)}=0.0555 \text { in }
then
t=(4 l x)^{1 / 2}=[4(0.281) 0.0555]^{1 / 2}=0.250 \text { in }
We have recognized the tooth as a cantilever beam of rectangular cross section, so the equivalent rotating-beam diameter must be obtained from Eq. (6–25):
d_{e}=0.808(h b)^{1 / 2} (6–25)
d_{e}=0.808(h b)^{1 / 2}=0.808(F t)^{1 / 2}=0.808[1.5(0.250)]^{1 / 2}=0.495 \text { in }
Then, Eq. (6–20) gives k_{b} as
k_{b}=\left\{\begin{array}{ll}(d / 0.3)^{-0.107}=0.879 d^{-0.107} & 0.11 \leq d \leq 2 \text { in } \\0.91 d^{-0.157} & 2<d \leq 10 \text { in } \\(d / 7.62)^{-0.107}=1.24 d^{-0.107} & 2.79 \leq d \leq 51 mm \\1.51 d^{-0.157} & 51<d \leq 254 mm\end{array}\right. ( 6–20)
k_{b}=\left(\frac{d_{e}}{0.30}\right)^{-0.107}=\left(\frac{0.495}{0.30}\right)^{-0.107}=0.948
The load factor k_{c} from Eq. (6–26) is unity. With no information given concerning temperature and reliability we will set k_{d}=k_{e}=1.
In general, a gear tooth is subjected only to one-way bending. Exceptions include idler gears and gears used in reversing mechanisms. We will account for one-way bending by establishing a miscellaneous-effects Marin factor k_{f} .
For one-way bending the steady and alternating stress components are \sigma_{a}=\sigma_{m} = \sigma / 2 \text { where } \sigma is the largest repeatedly applied bending stress as given in Eq. (14–7). If a material exhibited a Goodman failure locus,
k_{c}=\left\{\begin{array}{ll}1 & \text { bending } \\0.85 & \text { axial } \\0.59 & \text { torsion }^{17}\end{array}\right. (6–26)
\sigma=\frac{K_{v} W^{t} P}{F Y} (14–7)
\frac{S_{a}}{S_{e}^{\prime}}+\frac{S_{m}}{S_{u t}}=
Since S_{a} and S_{m} are equal for one-way bending, we substitute S_{a} for S_{m} and solve the preceding equation for S_{a} , giving
S_{a}=\frac{S_{e}^{\prime} S_{u t}}{S_{e}^{\prime}+S_{u t}}
Now replace S_{a} with σ/2, and in the denominator replace S_{e}^{\prime} with 0.5S_{u t} to obtain
\sigma=\frac{2 S_{e}^{\prime} S_{u t}}{0.5 S_{u t}+S_{u t}}=\frac{2 S_{e}^{\prime}}{0.5+1}=1.33 S_{e}^{\prime}
Now k_{f}=\sigma / S_{e}^{\prime}=1.33 S_{e}^{\prime} / S_{e}^{\prime}=1.33. a Gerber fatigue locus gives mean values of
\frac{S_{a}}{S_{e}^{\prime}}+\left(\frac{S_{m}}{S_{u t}}\right)^{2}=1
Setting S_{a}=S_{m} and solving the quadratic in S_{a} gives
S_{a}=\frac{S_{u t}^{2}}{2 S_{e}^{\prime}}\left(-1+\sqrt{1+\frac{4 S_{e}^{\prime 2}}{S_{u t}^{2}}}\right)
Setting S_{a}=\sigma / 2, S_{u t}=S_{e}^{\prime} / 0.5 gives
\sigma=\frac{S_{e}^{\prime}}{0.5^{2}}\left[-1+\sqrt{1+4(0.5)^{2}}\right]=1.66 S_{e}^{\prime}
and k_{f}=\sigma / S_{s}^{\prime}=1.66. Since a Gerber locus runs in and among fatigue data and Goodman does not, we will use k_{f}=1.66. The Marin equation for the fully corrected endurance strength is
\begin{aligned}S_{e} &=k_{a} k_{b} k_{c} k_{d} k_{e} k_{f} S_{e}^{\prime} \\&=0.934(0.948)(1)(1)(1) 1.66(27.5)=40.4 kpsi\end{aligned}
For stress, we will first determine the fatigue stress-concentration factor K_{f}. For a 20◦ full-depth tooth the radius of the root fillet is denoted r_{f}, where
r_{f}=\frac{0.300}{P}=\frac{0.300}{8}=0.0375 \text { in }
From Fig. A–15–6
\frac{r}{d}=\frac{r_{f}}{t}=\frac{0.0375}{0.250}=0.15
Since D/d =∞, we approximate with D/d = 3, giving K_{t}=1.68. From Fig. 6–20, q = 0.62. From Eq. (6–32)
K_{f}=1+q\left(K_{t}-1\right) \quad \text { or } \quad K_{f s}=1+q_{\text {shear }}\left(K_{t s}-1\right) (6–32)
K_{f}=1+(0.62)(1.68-1)=1.42
For a design factor of n_{d}=3, as used in Ex. 14–1, applied to the load or strength, the maximum bending stress is
\sigma_{\max }=K_{f} \sigma_{ all }=\frac{S_{e}}{n_{d}}
\sigma_{\text {all }}=\frac{S_{e}}{K_{f} n_{d}}=\frac{40.4}{1.42(3)}=9.5 kpsi
The transmitted load W^{t} is
W^{t}=\frac{F Y \sigma_{\text {all }}}{K_{v} P}=\frac{1.5(0.296) 9500}{1.52(8)}=347 lbf
and the power is, with V = 628 ft/min from Ex. 14–1,
h p=\frac{W^{t} V}{33000}=\frac{347(628)}{33000}=6.6 hp
Again, it should be emphasized that these results should be accepted only as preliminary estimates to alert you to the nature of bending in gear teeth.


Related Answered Questions
There will be many terms to obtain so use Figs. 14...
All of the parameters in this example are the same...
For through-hardened grade 1 steel the pinion stre...
From Fig. 14–5,
\left(S_{c}\right)_{...
Make the a priori decisions:
Function: 100 hp, 112...
The term moderate applications seems to imply that...
From Table A–5 we find the elastic constants to be...