Estimate the viscosity of toluene at 80^{\circ} C, using the value at 80^{\circ} C given in Example 8.2.
Question 8.3: Estimate the viscosity of toluene at 80ºC, using the value a...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
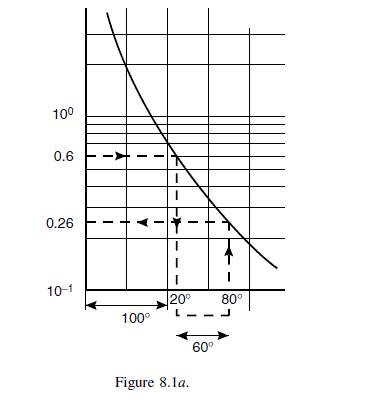
\text { Temperature increment } 80-20=60^{\circ} C \text {. }
\text { From Figure } 8.1 a \text {, viscosity at } 80^{\circ} C =0.26 mN s / m ^{2} \text {. }
Effect of pressure
The viscosity of a liquid is dependent on pressure as well as temperature, but the effect is not significant except at very high pressures. A rise in pressure of 300 bar is roughly equivalent to a decrease in temperature of 1^{\circ} C.
Mixtures
It is difficult to predict the viscosity of mixtures of liquids. Viscosities are rarely additive, and the shape of the viscosity-concentration curve can be complex. The viscosity of the mixture may be lower or, occasionally, higher than that of the pure components. A rough check on the magnitude of the likely error in a design calculation, arising from uncertainty in the viscosity of a mixture, can be made by using the smallest and largest values of the pure components in the calculation, and noting the result.
As an approximation, the variation can be assumed to be linear, if the range of viscosity is not very wide, and a weighted average viscosity calculated. For organic liquid mixtures a modified form of Souders’ equation can be used; using a mol fraction weighted average value for the viscosity constant for the mixture I_{m}, and the average molecular weight.
For a binary mixture equation 8.9 becomes:
\log \left(\log 10 \mu_{m}\right)=\rho_{m}\left[\frac{x_{1} I_{1}+x_{2} I_{2}}{x_{1} M_{1}+x_{2} M_{2}}\right] \times 10^{-3}-2.9 (8.10)
where \mu_{m} = viscosity of mixture,
\rho_{m} = density of mixture,
x_{1}, x_{2} = mol fraction of components,
M_{1}, M_{2} = molecular masses of components.
Bretsznajder (1971) gives a detailed review of the methods that have been developed for estimating the viscosity of mixtures, including methods for aqueous solutions and dispersions.
For heat-transfer calculations, Kern (1950) gives a rough rule of thumb for organic liquid mixtures:
\frac{1}{\mu_{m}}=\frac{w_{1}}{\mu_{1}}+\frac{w_{2}}{\mu_{2}} (8.11)
where w_{1}, w_{2} = mass fractions of the components 1 and 2,
\mu_{1}, \mu_{2} = viscosities of components 1 and 2.
Related Answered Questions
Diffusion volumes from Table 8.5; methanol:
...
Viscosity of ethanol at 20^{\circ} C , 1.2 ...
Calculation of parachor, CH _{3} OH...
Group
No. of
Total contribution
\Delta T[...
Use the binary Wilson A values given by Hirata (19...
Matrix of coefficients
j
1
2
3
4
i...
Toluene
Table 8.1. Contributions for ca...
\text { Density at } 30^{\circ} C =875 kg /...
Viscosity = 0.0134 mNs / m ^{2}
Spe...