Evaluating Performance of a Reheat Cycle with Turbine Irreversibility
Reconsider the reheat cycle of Example 8.3 but include in the analysis that each turbine stage has the same isentropic efficiency. (a) If \eta_{ t }=85 \%, determine the thermal efficiency. (b) Plot the thermal efficiency versus turbine stage isentropic efficiency ranging from 85 to 100%.
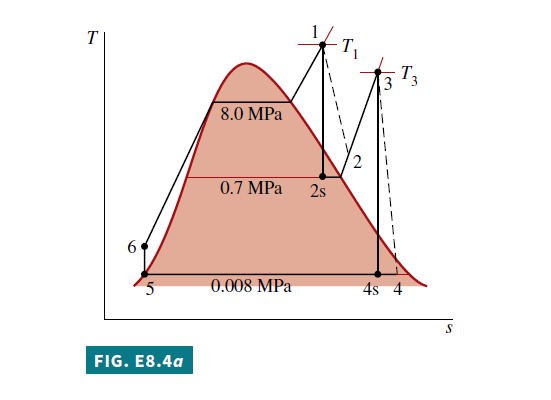
Known A reheat cycle operates with steam as the working fluid. Operating pressures and temperatures are specified. Each turbine stage has the same isentropic efficiency
Find If \eta_{ t }=85 \%, determine the thermal efficiency. Also plot the thermal efficiency versus turbine stage isentropic efficiency ranging from 85 to 100%.
Schematic and Given Data:
Engineering Model
1. As in Example 8.3, each component is analyzed as a control volume at steady state.
2. Except for the two turbine stages, all processes are internally reversible.
3. The turbine and pump operate adiabatically.
4. The condensate exits the condenser as saturated liquid.
5. Kinetic and potential energy effects are negligible.
Analysis
a. From the solution to Example 8.3, the following specific enthalpy values are known, in kJ/kg: h_{1}=3348.4, h_{2 s }=2741.8, h_{3}=3353.3, h_{4 s }=2428.5, h_{5}=173.88, h_{6}=181.94.
The specific enthalpy at the exit of the first-stage turbine, h_{2}, can be determined by solving the expression for the turbine isentropic efficiency, Eq. 8.9, to obtain
\eta_{ t }=\frac{\left(\dot{W}_{ t } / \dot{m}\right)}{\left(\dot{W}_{ t } / \dot{m}\right)_{ s }}=\frac{h_{1}-h_{2}}{h_{1}-h_{2 s }} (8.9)
\begin{aligned}h_{2} &=h_{1}-\eta_{ t }\left(h_{1}-h_{2 s }\right) \\&=3348.4-0.85(3348.4-2741.8)=2832.8 kJ / kg\end{aligned}
The specific enthalpy at the exit of the second-stage turbine can be found similarly:
\begin{aligned}h_{4} &=h_{3}-\eta_{ t }\left(h_{3}-h_{4 s }\right) \\&=3353.3-0.85(3353.3-2428.5)=2567.2 kJ / kg\end{aligned}
The thermal efficiency is then
\eta=\frac{\left(h_{1}-h_{2}\right)+\left(h_{3}-h_{4}\right)-\left(h_{6}-h_{5}\right)}{\left(h_{1}-h_{6}\right)+\left(h_{3}-h_{2}\right)} 1
=\frac{(3348.4-2832.8)+(3353.3-2567.2)-(181.94-173.88)}{(3348.4-181.94)+(3353.3-2832.8)}
=\frac{1293.6 kJ / kg }{3687.0 kJ / kg }=0.351(35.1 \%)
b. The IT code for the solution follows, where etat1 is \eta_{ t1}, etat2 is \eta_{ t2}, eta is \eta, \text { Wnet }=\dot{W}_{\text {net }} / \dot{m}, \text { and } \text { Qin }=\dot{Q}_{\text {in }} / \dot{m}.
Using the Explore button, sweep eta from 0.85 to 1.0 in steps of 0.01. Then, using the Graph button, obtain the following plot:
From Fig. E8.4b, we see that the cycle thermal efficiency increases from 0.351 to 0.403 as turbine stage isentropic efficiency increases from 0.85 to 1.00, as expected based on the results of Example 8.3 and part (a) of the present example. Turbine isentropic efficiency is seen to have a significant effect on cycle thermal efficiency.
1 Owing to the irreversibilities present in the turbine stages, the net work per unit of mass developed in the present case is significantly less than in the case of Example 8.3. The thermal efficiency is also considerably less.
Skills Developed
Ability to…
• sketch the T–s diagram of the Rankine cycle with reheat, including turbine and pump irreversibilities.
• fix each of the principal states and retrieve necessary property data.
• apply mass, energy, and entropy principles.
• calculate performance parameters for the cycle.
Quick Quiz
If the temperature T _{3} were increased to 480°C, would you expect the thermal efficiency to increase, decrease, or stay the same? Ans. Increase.
// Fix the states
T1 = 480// °C
p1 = 80 // bar
h1 = h_PT (“Water/Steam”, p1, T1)
s1 = s_PT (“Water/Steam”, p1, T1)
p2 = 7 // bar
h2s = h_Ps (“Water/Steam”, p2, s1)
etat1 = 0.85
h2 = h1 − etat1 * (h1 − h2s)
T3 = 440 // °C
p3 = p2
h3 = h_PT (“Water/Steam”, p3, T3)
s3 = s_PT (“Water/Steam”, p3, T3)
p4 = 0.08//bar
h4s = h_Ps (“Water/Steam”, p4, s3)
etat2 = etat1
h4 = h3 − etat2 * (h3 − h4s)
p5 = p4
h5 = hsat_Px (“Water/Steam”, p5, 0) // kJ/kg
v5 = vsat_Px (“Water/Steam”, p5, 0) // m3/kg
p6 = p1
h6 = h5 + v5 * (p6 − p5) * 100// The 100 in this
expression is a unit conversion factor.
// Calculate thermal efficiency
Wnet = (h1 − h2) + (h3 − h4) − (h6 − h5)
Qin = (h1 − h6) + (h3 − h2)
eta = Wnet/Qin