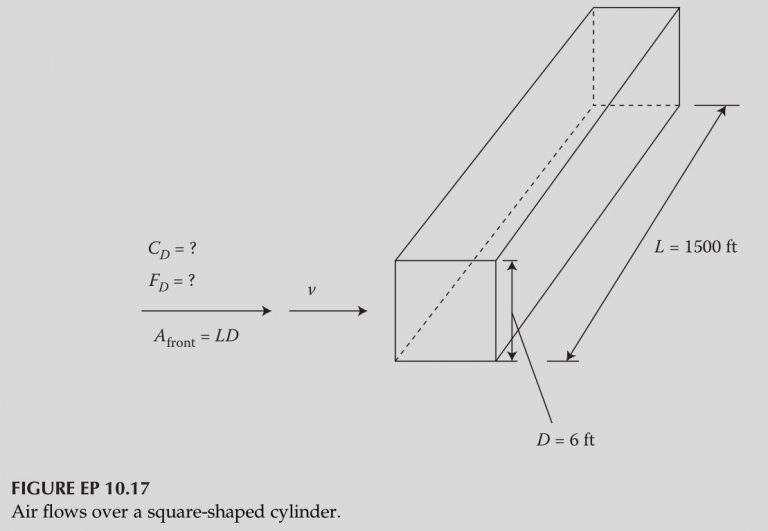
Figure 10.19 illustrates the variation of the drag coefficient, C_{D} for blunt (square shape) and streamlined (elliptical) 2-D bodies, for subsonic flow (M = v/c < 1), where compressibility effects are insignificant if M ≤ 0.5, while they are significant for M > 0.5. Consider a 1500-ft-long square-shaped cylinder with a side of 6 ft. Assume air at standard atmosphere at an altitude of 25,000 ft above sea level flows over the cylinder, as illustrated in Figure EP 10.17. (a) Determine the drag coefficient and the drag force if the velocity of flow over the cylinder is 400 ft/sec. (b) Determine the drag coefficient and the drag force if the velocity of flow over the cylinder is 800 ft/sec.
Question 10.17: Figure 10.19 illustrates the variation of the drag coefficie...

The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
(a)–(b) The frontal area is used to compute the drag force for the square cylinder, and the drag force is determined by applying Equation 10.12 F_{D} = C_{D} \frac{1}{2} \rho v^{2}A . The fluid properties for air at standard atmosphere at an altitude of 25,000ft above sea level is given in Table A.1 in Appendix A.
(a) The drag coefficient and the drag force for a velocity of flow over the cylinder of 400 ft/sec are determined as follows:
slug: = 1 lb \frac{sec^{2}}{ft} L: = 1500 ft D: = 6 ft A_{front}: = L.D = 9 \times 10^{3} ft^{2}
\rho : = 0.0010663 \frac{slug}{ft^{3}} c: = 1016.11 \frac{ft}{sec} E_{V}: = C^{2}. \rho = 1.101 \times 10^{3} \frac{lb}{ft^{2}}
V: = 400 \frac{ft}{sec} M: = \frac{V}{\sqrt{\frac{E_{V}}{\rho } } } = 0.394 C_{D}: = 2
Guess value: F_{D}: = 1 lb
Given
F_{D} = C_{D} \frac{1}{2} \rho.V^{2} . A_{front}
F_{D}: = Find (F_{D}) = 1.535 \times 10^{6} lb
(b) The drag coefficient and the drag force for a velocity of flow over the cylinder of 800 ft/sec are determined as follows:
V: = 800 \frac{ft}{sec} M: = \frac{V}{\sqrt{\frac{E_{V}}{\rho } } } = 0.787 C_{D}: = 2.1
Guess value: F_{D}: = 1 lb
Given
F_{D} = C_{D} \frac{1}{2} \rho.V^{2} . A_{front}
F_{D}: = Find (F_{D}) = 6.449 \times 10^{6} lb
Therefore, although the drag coefficient, C_{D} increases (from 2 to 2.1) with an increase in the velocity, v (from 400 ft/sec to 800 ft/sec) and thus an increase in the Mach number, M (from 0.384 to 0.787), the drag force, F_{D} increases (from 1.535 \times 10^{10} lb to 6.449 \times 10^{11} lb) with an increase in velocity, as F_{D} is directly proportional to V^{2} .
| Table A.1 | ||||||||
| Physical Properties for the International Civil Aviation Organization (ICAO) Standard Atmosphere as a Function of Elevation above Sea Level | ||||||||
| Elevation above Sea Level ft |
Temperature (θ) ^{\circ } F |
Absolute Pressure (p) psia |
Density \left(\rho \right) slug/ft^{3} |
Specific Weight \left(\gamma \right) lb/ft^{3} |
Absolute (Dynamic) Viscosity \left(\mu \right) 10^{-6} lb – sec/ft^{2} |
Kinematic Viscosity (ν) 10^{-3} ft^{2}/sec |
Speed of Sound (c) ft/sec |
Acceleration due to Gravity (g) ft/sec^{2} |
| 0 | 59.000 | 14.69590 | 0.002376800 | 0.0764720 | 0.37372 | 0.15724 | 1116.45 | 32.174 |
| 5000 | 41.173 | 12.22830 | 0.002048100 | 0.0658640 | 0.36366 | 0.17756 | 1097.08 | 32.158 |
| 10.000 | 23.355 | 10.10830 | 0.001755500 | 0.0564240 | 0.35343 | 0.20133 | 1077.40 | 32.142 |
| 15.000 | 5.545 | 8.29700 | 0.001496100 | 0.0480680 | 0.34302 | 0.22928 | 1057.35 | 32.129 |
| 20.000 | -12.255 | 6.75880 | 0.001267200 | 0.0406940 | 0.33244 | 0.26234 | 1039.94 | 32.113 |
| 25.000 | -30.048 | 5.46070 | 0.001066300 | 0.0342240 | 0.32166 | 0.30167 | 1016.11 | 32.097 |
| 30.000 | -47.048 | 4.37260 | 0.000890650 | 0.0285730 | 0.31069 | 0.34884 | 994.85 | 32.081 |
| 35.000 | -65.607 | 3.46760 | 0.000738190 | 0.0236720 | 0.29952 | 0.40575 | 973.13 | 32.068 |
| 40.000 | -69.700 | 2.73000 | 0.000587260 | 0.0188230 | 0.29691 | 0.50559 | 968.08 | 32.052 |
| 45.000 | -69.700 | 2.14890 | 0.000462270 | 0.0148090 | 0.29691 | 0.64230 | 968.08 | 32.036 |
| 50.000 | -69.700 | 1.69170 | 0.000363910 | 0.0116520 | 0.29691 | 0.81589 | 968.08 | 32.020 |
| 60.000 | -69.700 | 1.04880 | 0.000225610 | 0.0072175 | 0.29691 | 1.31600 | 968.08 | 31.991 |
| 70.000 | -67.425 | 0.65087 | 0.000139200 | 0.0044485 | 0.29836 | 2.14340 | 970.90 | 31.958 |
| 80.000 | -61.976 | 0.40632 | 0.000085707 | 0.0027366 | 0.30182 | 3.52150 | 997.62 | 31.930 |
| 90.000 | -56.535 | 0.25540 | 0.000053145 | 0.0016950 | 0.30525 | 5.74360 | 984.28 | 31.897 |
| 100.000 | -51.099 | 0.16160 | 0.000033182 | 0.0010575 | 0.30865 | 9.30180 | 990.91 | 31.868 |
| Elevation above Sea Level Km |
Temperature (θ) ^{\circ } C |
Absolute Pressure (p) kPa abs |
Density \left(\rho \right) kg/m^{3} |
Specific Weight \left(\gamma \right) N/m^{3} |
Absolute (Dynamic) Viscosity \left(\mu \right) 10^{-6} N – sec/m^{2} |
Kinematic Viscosity (ν) 10^{-6} m^{2}/sec |
Speed of Sound (c) m/sec |
Acceleration due to Gravity (g) m/sec^{2} |
| 0 | 15.000 | 101.325 | 1.22500 | 12.0131 | 17.894 | 14.607 | 340.294 | 9.80665 |
| 1 | 8.501 | 89.876 | 1.11170 | 10.8987 | 17.579 | 15.813 | 336.430 | 9.80360 |
| 2 | 2.004 | 79.501 | 1.00660 | 9.8652 | 17.260 | 17.147 | 332.530 | 9.80050 |
| 3 | -4.500 | 70.121 | 0.90925 | 8.9083 | 16.938 | 18.628 | 328.580 | 9.78740 |
| 4 | -10.984 | 61.66 | 0.81935 | 8.0250 | 16.612 | 20.275 | 324.590 | 9.79430 |
| 5 | -17.474 | 54.048 | 0.73643 | 7.2105 | 16.282 | 22.110 | 320.550 | 9.79120 |
| 6 | -23.693 | 47.217 | 0.66011 | 6.4613 | 15.949 | 24.161 | 316.450 | 9.78820 |
| 8 | -36.935 | 35.651 | 0.52579 | 5.1433 | 15.271 | 29.044 | 308.110 | 9.78000 |
| 10 | -49.898 | 26.499 | 0.41351 | 4.0424 | 14.577 | 35.251 | 299.530 | 9.77590 |
| 12 | -56.500 | 19.399 | 0.31194 | 3.0476 | 14.216 | 45.574 | 295.070 | 9.76970 |
| 14 | -56.500 | 14.17 | 0.22786 | 2.2247 | 14.216 | 62.391 | 295.070 | 9.76360 |
| 16 | -56.500 | 10.352 | 0.16647 | 1.6243 | 14.216 | 85.397 | 295.070 | 9.75750 |
| 18 | -56.500 | 7.565 | 0.12165 | 1.1862 | 14.216 | 116.860 | 295.070 | 9.75130 |
| 20 | -56.500 | 5.529 | 0.08891 | 0.8664 | 14.216 | 159.890 | 295.070 | 9.74520 |
| 25 | -51.598 | 2.549 | 0.04008 | 0.3900 | 14.484 | 361.350 | 298.390 | 9.73000 |
| 30 | -46.641 | 1.197 | 0.01841 | 0.1788 | 14.753 | 801.340 | 301.710 | 9.71470 |
Related Answered Questions
(a) In order to determine the lift force, Equation...
(a)–(b) The lift force is determined by applying E...
(a) The drag coefficient is determined by applying...
(a)–(b) The minimum takeoff and landing speed was ...
(a)–(b) The minimum takeoff and landing speed is d...
(a) The minimum takeoff and landing speed is deter...
(a) The lift coefficient is determined by applying...
(a)–(b) The planform area is used to compute the d...
(a) The frontal area is used to compute the drag f...
(a)–(b) The frontal area is used to compute the dr...