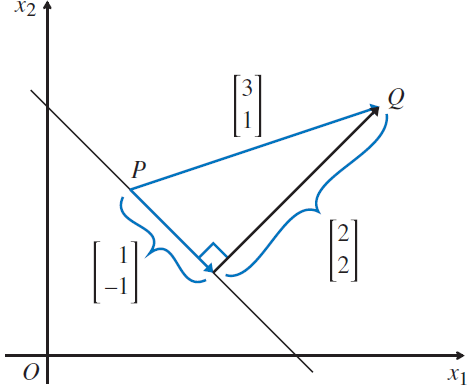
Find the distance from Q(4, 3) to the line x = [1 2] + t[-1 1], t ∈ R.

Question

Find the distance from Q(4, 3) to the line [latex]\vec{x} = \left [ \begin{matrix} 1 \ 2 \end{matrix} ight ] + t\left [ \begin{matrix} -1 \ 1 \end{matrix} ight ] , t\in \mathbb{R}.[/latex]

Accepted Answer

We pick the point P(1, 2) on the line. Then, [latex]\vec{PQ} = \left [ \begin{matrix} 4-1 \ 3-2 \end{matrix} ight ] = \left [ \begin{matrix} 3 \ 1 \end{matrix} ight ].[/latex] So, the distance is

[latex]\left\|perp_{\vec{d} } \left(\vec{PQ} ight) ight\| = \left\|\vec{PQ} - proj_{d}\left(\vec{PQ} ight) ight\|[/latex]

[latex]= \left\|\left [ \begin{matrix} 3 \ 1 \end{matrix} ight ] - \left(\frac{-3+1}{1+1} ight)\left [ \begin{matrix} -1 \ 1 \end{matrix} ight ] ight\|[/latex]

[latex]= \left\|\left [ \begin{matrix} 3 \ 1 \end{matrix} ight ] +\left [ \begin{matrix} -1 \ 1 \end{matrix} ight ] ight\| = \left\|\left [ \begin{matrix} 2 \ 2 \end{matrix} ight ] ight\| = 2\sqrt{2}[/latex]

Question 1.5.9: Find the distance from Q(4, 3) to the line x = [1 2] + t[-1 ...

Related Answered Questions