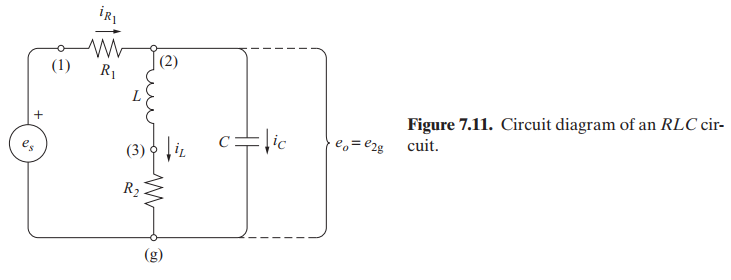
Find the input–output differential equation relating e_{o} to e_{s} for the simple RLC circuit shown in Fig. 7.11.
Question 7.1: Find the input–output differential equation relating eo to e...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
For the source,
e_{s} =e_{1g}. (7.24)
For the resistor R_{1},
i_{R1} =\frac{1}{R_{1} } \left(e_{1g}-e_{2g}\right) . (7.25)
For the inductor L,
e_{2g}-e_{3g}=\frac{di_{L} }{dt} . (7.26)
For the resistor R_{2},
e_{3g}=R_{2} i_{L} . (7.27)
For the capacitor C,
i_{c} =C\frac{de_{2g} }{dt} . (7.28)
At node 2,
i_{R1} =i_{L} +i_{C} . (7.29)
Equations (7.24)–(7.29) comprise a set of six equations involving six unknown variables: e_{1g}, e_{2g}, e_{3g}, i_{R1}, i_{L}, and i_{C}. (Note that using i_{L} to describe the current through both L and R_{2} satisfies Kirchhoff’s law at node 3 and eliminates one variable and one equation.)
The node method may be applied to node 2 to eliminate the unwanted variables e_{1g}, e_{3g}, i_{R1}, i_{L}, and i_{C}. Substituting for i_{R1} from Eq. (7.25) and for i_{C} from Eq. (7.28) into Eq. (7.29) yields
\frac{1}{R_{1} } \left(e_{1g} -e_{2g} \right) =i_{L} +C\frac{de_{2g} }{dt} . (7.30)
Then, using Eq. (7.24) for e_{1g} and rearranging Eq. (7.30) yields
i_{L}=\frac{1}{R_{1} }e_{s}- \frac{1}{R_{1} }e_{2g} -C\frac{de_{2g} }{dt} . (7.31)
Differentiating Eq. (7.31) with respect to time gives
\frac{di_{L} }{dt} =\left(\frac{1}{R_{1} } \right) \frac{de_{s} }{dt} -\left(\frac{1}{R_{1} } \right) \frac{de_{2g} }{dt}-C\frac{d^{2}e_{2g} }{dt^{2} } . (7.32)
Combine Eqs. (7.26) and (7.27) to solve for e_{2g}:
e_{2g}=L \frac{di_{L} }{dt}+R_{2} i_{L} . (7.33)
Substitution from Eqs. (7.31) and (7.32) into Eq. (7.33) then eliminates i_{L}:
e_{2g}=\left(\frac{L}{R_{1} } \right) \left(\frac{de_{s} }{dt}-\frac{de_{2g} }{dt} \right) -LC\frac{d^{2}e_{2g} }{dt^{2} } +\left(\frac{R_{2} }{R_{1} } \right) \left(e_{s}-e_{2g} \right) -R_{2} C\frac{de_{2g} }{dt}. (7.34)
Collecting terms and noting that e_{o} is the same as e_{2g}, we have
LC\frac{d^{2}e_{o} }{dt^{2} }+\left(\frac{L}{R_{1} }+R_{2}C \right) \frac{de_{o} }{dt} +\left(1+\frac{R_{2} }{R_{1} } \right) e_{o} =\frac{R_{2} }{R_{1}}e_{s} +\frac{L}{R_{1} } \frac{de_{s} }{dt} . (7.35)


Related Answered Questions
(a) In general, the state-variable for a capacitor...
Use Kirchhoff’s voltage law to write
e_{s} ...
The circuit shown in Fig. 7.22 is similar to the i...
Here the loop method is used and the elemental equ...