Find the magnetic field of a very long solenoid, consisting of n closely wound turns per unit length on a cylinder of radius R, each carrying a steady current I (Fig. 5.34). [The point of making the windings so close is that one can then pretend each turn is circular. If this troubles you (after all, there is a net current I in the direction of the solenoid’s axis, no matter how tight the winding), picture instead a sheet of aluminum foil wrapped around the cylinder, carrying the equivalent uniform surface current K = nI (Fig. 5.35). Or make a double winding, going up to one end and then—always in the same sense— going back down again, thereby eliminating the net longitudinal current. But, in truth, this is all unnecessary fastidiousness, for the field inside a solenoid is huge (relatively speaking), and the field of the longitudinal current is at most a tiny refinement.]
Question 5.9: Find the magnetic field of a very long solenoid, consisting ...

Learn more on how we answer questions.
First of all, what is the direction of B? Could it have a radial component? No. For suppose B_{s} were positive; if we reversed the direction of the current, B_{s} would then be negative. But switching I is physically equivalent to turning the solenoid upside down, and that certainly should not alter the radial field. How about a “circumferential” component? No. For B_{\phi } would be constant around an Amperian loop concentric with the solenoid (Fig. 5.36), and hence
\oint{\pmb{B}}.d\pmb{I}=B_{\phi }(2\pi s)=\mu _{0}I_{enc}=0,since the loop encloses no current.
So the magnetic field of an infinite, closely wound solenoid runs parallel to the axis. From the right-hand rule, we expect that it points upward inside the solenoid and downward outside. Moreover, it certainly approaches zero as you go very far
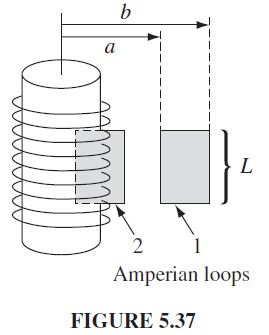
away. With this in mind, let’s apply Ampère’s law to the two rectangular loops in Fig. 5.37. Loop 1 lies entirely outside the solenoid, with its sides at distances a and b from the axis:
\oint{\pmb{B}}.d\pmb{I}=[B(a)-B(b)]L=\mu _{0}I_{enc}=0,so
B(a)=B(b)Evidently the field outside does not depend on the distance from the axis. But we agreed that it goes to zero for large s. It must therefore be zero everywhere! (This astonishing result can also be derived from the Biot-Savart law, of course, but it’s much more difficult. See Prob. 5.46.)
As for loop 2, which is half inside and half outside, Ampère’s law gives
where B is the field inside the solenoid. (The right side of the loop contributes nothing, since B = 0 out there.) Conclusion:
\pmb{B}=\begin{cases} μ_{0}nI\hat{\pmb{Z}}, inside the solenoid, \\ 0, outside the solenoid.\end{cases} (5.59)
Notice that the field inside is uniform—it doesn’t depend on the distance from the axis. In this sense the solenoid is to magnetostatics what the parallel-plate capacitor is to electrostatics: a simple device for producing strong uniform fields.