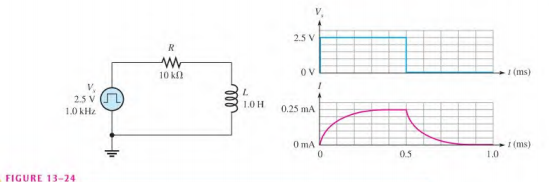
For the circuit in Figure 13-24, what is the current at 0.1 ms and 0.6 ms?
Question 13.8: For the circuit in Figure 13-24, what is the current at 0.1 ...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
The RL time constant for the circuit is
\tau =\frac{L}{R}=\frac{1.0 \ mH}{10 \ K\Omega } = 0.1 \ msIf the square-wave generator period is long enough for the current to reach its maximum value in 5\tau , the current will increase exponentially and during each time constant interval will have a value equal to the percentage of the final current given in Table 13-1:
| NUMBER OF TIME CONSTANTS |
APPROXIMATE % OF FINAL CURRENT |
| 1 | 63 |
| 2 | 86 |
| 3 | 95 |
| 4 | 98 |
| 5 | 99 (considered 100%) |
. The final current is
I_{F}= \frac{V_{S}}{R}= \frac{2.5 \ V}{10 \ k\Omega }= 0.25 \ mAThe current at 0.1 ms is
i = 0.63(0.25 mA) = 0.158 mA
At 0.6 ms, the square-wave input has been at the 0 V level for 0.1 ms, or 1 \tau ; and the current decreases from the maximum value toward its final value of 0 mA by 63%. Therefore,
i = 0.25 mA – 0.63(0.25 mA) = 0.092 mA
Related Answered Questions
The reactances of the individual inductors are the...
Convert 10 kHz to 10\times 10^{3}Hz...
First, calculate the inductive reactance and curre...
The RL time constant is
\tau =\frac{L}{R}=\...
(a) \tau =\frac{L}{R}=\frac{15 \ mH}{33 \ K...
The RL time constant is
\tau =\frac{L}{R}=\...
Convert 10 kHz to 10\times 10^{3} H...
v_{ind}= L\left(\frac{di}{dt} \right)= (1 \...
v_{ind}= N\left(\frac{d\phi }{dt} \right)= ...