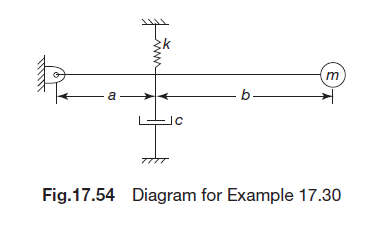
For the system shown in Fig.17.54, determine the natural frequency of damped vibrations and critical damping coefficient
Question 17.30: For the system shown in Fig.17.54, determine the natural fre...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
The equation of motion is:
m(a+b)^{2} \ddot{\theta}+c a^{2} \dot{\theta}+k a^{2} \theta=0 .
Comparing with the standard equation of motion, we have
I=m(a+b)^{2} .
c_{t e}=c a^{2} .
q_{e}=k a^{2} .
Undamped natural frequency, \omega_{n}=\sqrt{\frac{q_{e}}{I}} .
=\sqrt{\frac{k a^{2}}{m(a+b)^{2}}} .
=\frac{a}{(a+b)} \sqrt{\frac{k}{m}} rad / s .
\text { Critical damping coefficient, } c_{t c}=2 I \omega_{n} .
=2 m(a+b)^{2}\left[\left(\frac{a}{a+b}\right) \sqrt{\frac{k}{m}}\right] .
=2 a(a+b) \sqrt{k m} .
Damping factor, \zeta=\frac{c_{t e}}{c_{t c}} .
=\frac{c a^{2}}{2 a(a+b) \sqrt{k m}} .
=\frac{c a}{2(a+b) \sqrt{k m}} .
\text { Damped natural frequency, } \omega_{d}=\omega_{n} \sqrt{1-\zeta^{2}} .
=\left(\frac{a}{a+b}\right) \sqrt{\frac{k}{m}} \sqrt{1-\frac{c^{2} a^{2}}{4(a+b)^{2} k m}} .
=\frac{a}{2(a+b)^{2} m} \sqrt{4(a+b)^{2} k m-c^{2} a^{2}} .
Related Answered Questions
The equation of motion is:
m l^{2} \ddot{\...
The equation of motion is,
J \ddot{\theta}...
\omega_{n}=\sqrt{\frac{g}{\delta_{s t}}}=\...
(a) Force in each spring = 2W.
\text { Def...
Force in spring 1, F_{1}=\frac{W b}{a+b...
Let l = length of U-tube containing the fluid
A = ...
Deflection of a helical spring under axial load is...
Force in spring 1, F_{1}=m g .
...
Given: m=5 kg , f_{d}=\frac{50}...