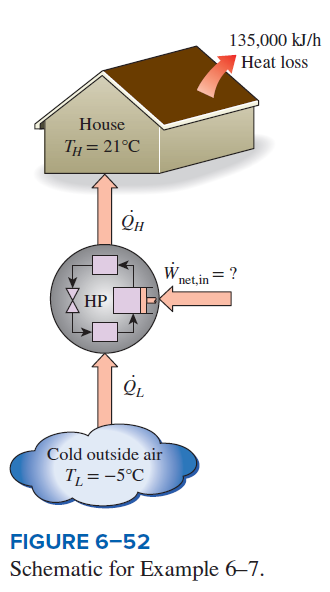
Heating a House with a Carnot Heat Pump
A heat pump is to be used to heat a house during the winter, as shown in Fig. 6–52. The house is to be maintained at 21°C at all times. The house is estimated to be losing heat at a rate of 135,000 kJ/h when the outside temperature drops to –5°C. Determine the minimum power required to drive this heat pump.
A heat pump maintains a house at a constant temperature. The required minimum power input to the heat pump is to be determined.
Assumptions Steady operating conditions exist.
Analysis The heat pump must supply heat to the house at a rate of \dot{Q}_{H}=135,000 \mathrm{~kJ} / \mathrm{h}= 37.5 \mathrm{~kW}. The power requirements are minimum when a reversible heat pump is used to do the job. The COP of a reversible heat pump operating between the house and the outside air is
\mathrm{COP}_{\mathrm{HP}, \mathrm{rev}}=\frac{1}{1-T_{L} / T_{H}}=\frac{1}{1-(-5+273 \mathrm{~K}) /(21+273 \mathrm{~K})}=11.3
Then, the required power input to this reversible heat pump becomes
\dot{W}_{\text {net,in }}=\frac{\dot{Q}_{H}}{\mathrm{COP}_{\mathrm{HP}}}=\frac{37.5 \mathrm{~kW}}{11.3}=3.32 \mathrm{~kW}
Discussion This reversible heat pump can meet the heating requirements of this house by consuming electric power at a rate of 3.32 \mathrm{~kW} only. If this house were to be heated by electric resistance heaters instead, the power consumption would jump up 11.3 times to 37.5 \mathrm{~kW}. This is because in resistance heaters the electric energy is converted to heat at a one-to-one ratio. With a heat pump, however, energy is absorbed from the outside and carried to the inside using a refrigeration cycle that consumes only 3.32 kW. Notice that the heat pump does not create energy. It merely transports it from one medium (the cold outdoors) to another (the warm indoors).