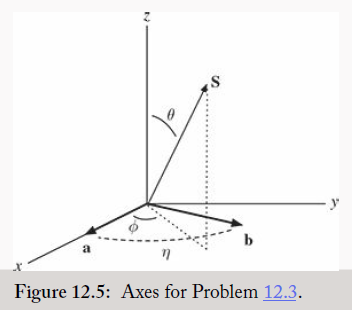
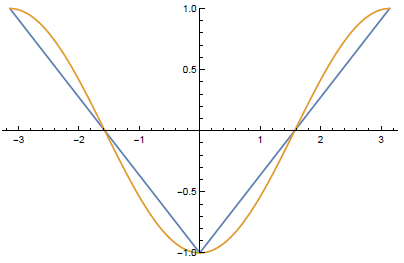(a) Reading from the figure, a =\hat{i}, b =\cos \eta \hat{i}+\sin \eta \hat{j}, \quad S _{a}=S_{a}(\sin \theta \cos \phi \hat{i}+\sin \theta \sin \phi \hat{j}+\cos \theta \hat{k})=- S _{b} , so
a \cdot S _{a}=S_{a} \sin \theta \cos \phi ,
b \cdot S _{b}=-S_{a} \sin \theta(\cos \phi \cos \eta+\sin \phi \sin \eta)=-S_{a} \sin \theta \cos (\phi-\eta) .
But \sin \theta \geq 0 \text { (since } \theta \text { is between } 0 \text { and } \pi \text { ) } , so
A=\operatorname{sign}\left( a \cdot S _{a}\right)=\operatorname{sign}(\cos \phi), B=-\operatorname{sign}((\cos (\phi-\eta)), \text { and hence } A( a , \lambda) B( b , \lambda)=-\operatorname{sign}[\cos \phi \cos (\phi-\eta)] .
\text { (b) } P( a , b )=\langle A( a , \lambda) B( b , \lambda)\rangle=\frac{1}{4 \pi} \int[A( a , \lambda) B( b , \lambda)] \sin \theta d \theta d \phi=-\frac{2}{4 \pi} \int_{0}^{2 \pi} \operatorname{sign}[\cos \phi \cos (\phi-\eta)] d \phi \text {. }
Now, \cos \phi \text { is positive unless } \frac{\pi}{2}<\phi<\frac{3 \pi}{2}, \text { and } \cos (\phi-\eta) \text { is positive unless } \frac{\pi}{2}+\eta<\phi<\frac{3 \pi}{2}+\eta .
Assume first that 0<\eta<\frac{\pi}{2} , and chop the integral into eight segments, writing (++) to indicate that \cos \phi is positive and \cos (\phi-\eta) is positive, etc.:
P( a , b )=-\frac{1}{2 \pi}\left\{\int_{0}^{\eta}(++) d \phi+\int_{\eta}^{\pi / 2}(++) d \phi+\int_{\pi / 2}^{\pi / 2+\eta}(-+) d \phi+\int_{\pi / 2+\eta}^{\pi}(–) d \phi\right.
\left.+\int_{\pi}^{\pi+\eta}(–) d \phi+\int_{\pi+\eta}^{3 \pi / 2}(–) d \phi+\int_{3 \pi / 2}^{3 \pi / 2+\eta}(+-) d \phi+\int_{3 \pi / 2+\eta}^{2 \pi}(++) d \phi\right\} .
=-\frac{1}{2 \pi}\left\{(\eta-0)+\left(\frac{\pi}{2}-\eta\right)-\left(\frac{\pi}{2}+\eta-\frac{\pi}{2}\right)+\left(\pi-\frac{\pi}{2}-\eta\right)+(\pi+\eta-\pi)+\left(\frac{3 \pi}{2}-\pi-\eta\right)\right.
\left.-\left(\frac{3 \pi}{2}+\eta-\frac{3 \pi}{2}\right)+\left(2 \pi-\frac{3 \pi}{2}-\eta\right)\right\}=-\frac{1}{2 \pi}(2 \pi-4 \eta)=\frac{2 \eta}{\pi}-1 .
That’s for 0<\eta<\frac{\pi}{2} ; \text { for } \frac{\pi}{2}<\eta<\pi we have:
P( a , b )=-\frac{1}{2 \pi}\left\{\int_{0}^{\eta-\pi / 2}(+-) d \phi+\int_{\eta-\pi / 2}^{\pi / 2}(++) d \phi+\int_{\pi / 2}^{\eta}(-+) d \phi+\int_{\eta}^{\pi}(-+) d \phi\right.
\left.+\int_{\pi}^{\eta+\pi / 2}(-+) d \phi+\int_{\eta+\pi / 2}^{3 \pi / 2}(–) d \phi+\int_{3 \pi / 2}^{\eta+\pi}(+-) d \phi+\int_{\eta+\pi}^{2 \pi}(+-) d \phi\right\} .
=-\frac{1}{2 \pi}\left\{-\left(\eta-\frac{\pi}{2}-0\right)+\left(\frac{\pi}{2}-\eta+\frac{\pi}{2}\right)-\left(\eta-\frac{\pi}{2}\right)-(\pi-\eta)-\left(\eta+\frac{\pi}{2}-\pi\right)+\left(\frac{3 \pi}{2}-\eta-\frac{\pi}{2}\right)\right.
\left.-\left(\eta+\pi-\frac{3 \pi}{2}\right)-(2 \pi-\eta-\pi)\right\}=-\frac{1}{2 \pi}(2 \pi-4 \eta)=\frac{2 \eta}{\pi}-1 . (same as before).
The average is an even function of η, so the general result \text { (for } \left.-\frac{\pi}{2}<\eta<\frac{\pi}{2}\right) \text { is } \frac{2|\eta|}{\pi}-1 \text {. }
(c) The quantum prediction (Equation 12.4) is P( a , b )=-\cos \eta ; plotting the two:
P( a , b )=- a \cdot b (12.4).
\operatorname{Plot}\left[\left\{\frac{2 Abs [ x ]}{\pi}-1,-\cos [ x ]\right\},\{ x ,-\pi, \pi\}, \text { PlotRange } \rightarrow\{-1,1\}\right] .
They agree at \eta=0, \pm \frac{\pi}{2}, \text { and } \pm \pi .
(d) In this example Bell’s inequality says \left|\frac{2}{\pi}\right| \eta_{a b}\left|-1-\frac{2}{\pi}\right| \eta_{a c}|+1| \leq 1+\frac{2}{\pi}\left|\eta_{b c}\right|-1, \text { or }
|| \eta_{a b}|-| \eta_{a c}|| \leq\left|\eta_{b c}\right| ,
where all angles are in the range [-\pi, \pi] ]. Now, first assume that \left|\eta_{a b}\right|>\left|\eta_{a c}\right| . In that case
\left|\eta_{a b}\right| \leq\left|\eta_{a c}\right|+\left|\eta_{c b}\right| .
On the other hand, if \left|\eta_{a c}\right|>\left|\eta_{a b}\right| .
\left|\eta_{a c}\right| \leq\left|\eta_{a b}\right|+\left|\eta_{b c}\right| .
In either case, the equation says that one angle is smaller than the sum of the other two. This is clearly correct: the vectors a, b, and c define points a, b, and c on a unit sphere, and the angles between the vectors are proportional to the lengths of the great arcs connecting those points. So the inequality just expresses the fact that walking \straight” from a to b is shorter than walking from a to c and c to b (unless c happens to lie on your path in which case it is the same distance).