(O’Neill and Reese, 1999)
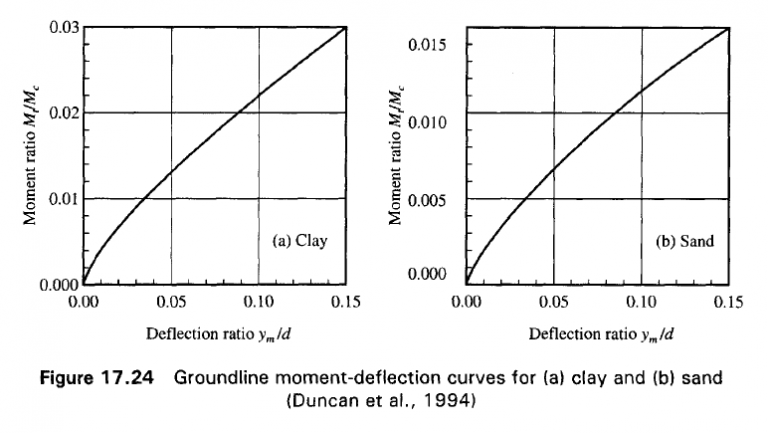
Refer to Fig. Ex. 17.11. Determine for a free-head pier (a) the groundline deflection, and (b) the maximum bending moment. Use the Duncan et al., (1994) method. Assume R_{I}=1 in the Eqs (17.44) and (17.45).
P_{c}=1.57 d^{2}\left(E R_{I}\right) \frac{\gamma^{\prime} d \phi^{\prime} K_{p}}{E R_{I}}^{0.57} (17.44)
M_{c}=1.33 d^{3}\left(E R_{I}\right) \frac{\gamma^{\prime} d \phi^{\prime} K_{p}}{E R_{I}}^{0.40} (17.45)
Substituting in Eqs (17.42) and (17.43)
P_{c}=7.34 d^{2}\left(E R_{I}\right) \frac{c_{u}}{E R_{I}}^{0.68} (17.42)
M_{c}=3.86 d^{3}\left(E R_{I}\right) \frac{c_{u}}{E R_{I}}^{0.46} (17.43)
P_{c}=7.34 \times(0.80)^{2}\left[25 \times 10^{3} \times(1)\right] \frac{0.06}{25 \times 10^{3}}^{0.68}=17.72 MN
M_{c}=3.86(0.80)^{3}\left[25 \times 10^{3} \times(1)\right] \frac{0.06}{25 \times 10^{3}}^{0.46}=128.5 MN – m
Now \frac{P_{t}}{P_{c}}=\frac{0.080}{17.72}=0.0045, \frac{M_{t}}{M_{c}}=\frac{0.4}{128.5}=0.0031
Step1
From Fig. 17.23a for \frac{P_{t}}{P_{c}}=0.0045
\frac{y_{p}}{d}=0.003 \text { or } y_{p}=0.003 \times 0.8 \times 10^{3}=2.4 mm
From Fig. 17.24a, M_{t} / M_{c}=0.0031
\frac{y_{m}}{d}=0.006 \text { or } y_{m}=0.006 d=0.006 \times 0.8 \times 10^{3}=4.8 mm
Step 2
From Fig. 17.23(a) for y_{m} / d=0.006, P_{m} / P_{c}=0.0055
From Fig. 17.24(a), for y_{p} / d=0.003, M_{p} / M_{c}=0.0015.
Step 3
The shear loads P_{t} \text { and } P_{m} applied at ground level, may be expressed as
\frac{P_{t}}{P_{c}}+\frac{P_{m}}{P_{c}}=0.0045+0.0055=0.01
From Fig. 17.23,
\frac{y_{t p}}{d}=0.013 \text { for } \frac{P_{t}+P_{m}}{P_{c}}=0.01
or y_{t p}=0.013 \times(0.80) \times 10^{3}=10.4 mm
Step 4
In the same way as in Step 3
\frac{M_{t}}{M_{c}}+\frac{M_{p}}{M_{c}}=0.0031+0.0015=0.0046
From Fig. 17.24a \frac{y_{t m}}{d}=\frac{y_{m}+y_{p m}}{d}=0.011
Hence y_{t m}=0.011 \times 0.8 \times 10^{3}=8.8 mm
Step 5
From Eq. (17.50)
y_{t}=\frac{y_{t p}+y_{t m}}{2}=\frac{\left(y_{p}+y_{m p}\right)+\left(y_{m}+y_{p m}\right)}{2} (17.50)
y_{t}=\frac{y_{t p}+y_{t m}}{2}=\frac{10.4+8.8}{2}=9.6 mm
Step 6
The maximum moment for the combined shear load and moment at the pier head may be calculated in the same way as explained in Chapter 16. M_{(\max )} as obtained is
M_{\max }=470.5 kN – m
This occurs at a depth of 1.3 m below ground level.
