Rigid bar ABCD is loaded and supported as shown in Figure P5.65. Bar (1) is made of bronze [E = 100 GPa, α = 16.9 × $10^{-6}$ /°C] and has a cross-sectional area of 400 $mm ^{2}$ . Bar (2) is made of aluminum [E = 70 GPa, α = 22.5 × $10^{-6}$ /°C] and has a cross-sectional area of 600 $mm ^{2}$ . Bars (1) and (2) are initially unstressed. After the temperature has increased by 40°C, determine:
(a) the stresses in bars (1) and (2).
(b) the vertical deflection of point A.

Question

Rigid bar ABCD is loaded and supported as shown in Figure P5.65. Bar (1) is made of bronze [E = 100 GPa, α = 16.9 × [latex]10^{-6}[/latex]/°C] and has a cross-sectional area of 400 [latex]mm ^{2}[/latex] . Bar (2) is made of aluminum [E = 70 GPa, α = 22.5 × [latex]10^{-6}[/latex]/°C] and has a cross-sectional area of 600 [latex]mm ^{2}[/latex] . Bars (1) and (2) are initially unstressed. After the temperature has increased by 40°C, determine:
(a) the stresses in bars (1) and (2).
(b) the vertical deflection of point A.

Accepted Answer

Equilibrium
Consider a FBD of the rigid bar. Assume tension forces in members (1) and (2). A moment equation about pin D gives the best information for this situation:

[latex]\Sigma M_{D}=(3 m ) F_{1}-(1 m ) F_{2}=0 \quad herefore F_{2}=3 F_{1}[/latex] (a)

Geometry of Deformations Relationship
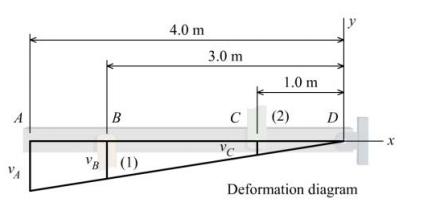
Draw a deformation diagram of the rigid bar. The deflections of the rigid bar are related by similar triangles:

[latex]\frac{v_{A}}{4 m }=\frac{v_{B}}{3 m }=\frac{v_{C}}{1 m }[/latex] (b)

There are no gaps, clearances, or other misfits at pins B and C; therefore, Eq. (b) can be rewritten in terms of the member deformations as:

[latex]\frac{-\delta_{1}}{3 m }=\frac{\delta_{2}}{1 m } \quad herefore \delta_{1}=-3 \delta_{2}[/latex] (c)

Note: To understand the negative sign associated with [latex]\delta_{1}[/latex], see Section 5.5 for discussion of statically indeterminate rigid bar configurations with opposing members.

Force-Temperature-Deformation Relationships

[latex]\delta_{1}=\frac{F_{1} L_{1}}{A_{1} E_{1}}+\alpha_{1} \Delta T_{1} L_{1} \quad \delta_{2}=\frac{F_{2} L_{2}}{A_{2} E_{2}}+\alpha_{2} \Delta T_{2} L_{2}[/latex] (d)

Compatibility Equation

[latex]\frac{F_{1} L_{1}}{A_{1} E_{1}}+\alpha_{1} \Delta T_{1} L_{1}=-3\left[\frac{F_{2} L_{2}}{A_{2} E_{2}}+\alpha_{2} \Delta T_{2} L_{2} ight][/latex] (e)

Solve the Equations
For this situation, [latex]\Delta T_{1}=\Delta T_{2}=\Delta T=40^{\circ} C[/latex] . Substitute Eq. (a) into Eq. (e):

[latex]\frac{F_{1} L_{1}}{A_{1} E_{1}}+\alpha_{1} \Delta T L_{1}=-3\left[\frac{\left(3 F_{1} ight) L_{2}}{A_{2} E_{2}}+\alpha_{2} \Delta T L_{2} ight][/latex]

and solve for [latex]F_{1}[/latex]:

[latex]\begin{aligned}F_{1} &=-\frac{\Delta T\left(3 \alpha_{2} L_{2}+\alpha_{1} L_{1} ight)}{\frac{L_{1}}{A_{1} E_{1}}+\frac{9 L_{2}}{A_{2} E_{2}}} \&=-\frac{\left(40^{\circ} C ight)\left[3\left(22.5 imes 10^{-6} /{ }^{\circ} C ight)(920 mm )+\left(16.9 imes 10^{-6} /{ }^{\circ} C ight)(840 mm ) ight]}{\frac{940 mm }{\left(400 mm ^{2} ight)\left(100,000 N / mm ^{2} ight)}+\frac{9(920 mm )}{\left(600 mm ^{2} ight)\left(70,000 N / mm ^{2} ight)}} \&=-13,990 N =-13.990 kN\end{aligned}[/latex]

Backsubstitute into Eq. (a) to find [latex]F_{2}[/latex] = −41.970 kN.

(a) Normal Stresses
The normal stresses in each axial member can now be calculated:

[latex]\begin{aligned}&\sigma_{1}=\frac{F_{1}}{A_{1}}=\frac{-13,990 N }{400 mm ^{2}}=35.0 MPa ( C ) \&\sigma_{2}=\frac{F_{2}}{A_{2}}=\frac{-41,970 N }{600 mm ^{2}}=70.0 MPa ( C )\end{aligned}[/latex]

(b) Deflection of the rigid bar at A
Calculate the deformation of one of the axial members, say member (1):

[latex]\begin{aligned}\delta_{1} &=\frac{F_{1} L_{1}}{A_{1} E_{1}}+\alpha_{1} \Delta T_{1} L_{1} \&=\frac{(-13,990 N )(840 mm )}{\left(400 mm ^{2} ight)\left(100,000 N / mm ^{2} ight)}+\left(16.9 imes 10^{-6} /{ }^{\circ} C ight)\left(40^{\circ} C ight)(840 mm ) \&=0.27405 mm\end{aligned}[/latex]

Since there are no gaps at pin B, the rigid bar deflection at B is equal to the deformation of member (1);
therefore, [latex]v_{B}=\delta_{1}=0.27405 mm ext { (upward). }[/latex] From similar triangles, the deflection of the rigid bar at A is related to [latex]v_{B}[/latex] by:

[latex]\frac{v_{A}}{4 m}=\frac{v_{B}}{3 m}[/latex]

The deflection of the rigid bar at A is thus:

[latex]v_{A}=\frac{4 m }{3 m } v_{B}=\frac{4 m }{3 m }(0.27405 mm )=0.365 mm \uparrow[/latex]

Question 5.65: Rigid bar ABCD is loaded and supported as shown in Figure P5...

Related Answered Questions