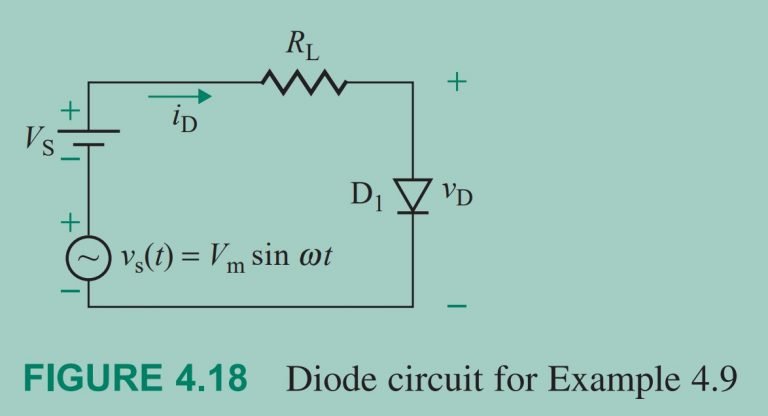
Small-signal analysis of a diode circuit The diode circuit shown in Fig. 4.18 has V_{ S }=10 V , V_{ m }=50 mV \text {, and } R_{ L }=1 k \Omega . Use the Q-point found in Example 4.7 by mathematical method to determine the instantaneous diode voltage {v}_D . Assume an emission coefficient of n = 1.84.
Question 4.9: Small-signal analysis of a diode circuit The diode circuit s...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
V_{ T }=25.8 mV , n=1.84, V_{ S }=10 V \text {, and } R_{ L }=1 k \Omega . The iterations of the Q-point analysis in Example 4.7 gave V_{ D }=0.7148 V \text { and } I_{ D }=9.284 mA . Using Eq. (4.27), we can find the AC resistance r_{ d } from
r_{ d }=R_{ D }=\frac{1}{g_{ d }}=\frac{n V_{ T }}{i_{ D }+I_{ S }} \approx \frac{n V_{ T }}{I_{ D }} \text { since } i_{ D }=I_{ D }, \text { and } I_{ D } \gg I_{ S } (4.27)
r_{ d }=\frac{n V_{ T }}{I_{ D }}=\frac{1.84 \times 25.8 \times 10^{-3}}{\left(9.284 \times 10^{-3}\right)}=5.11 \Omega
The AC equivalent circuit is shown in Fig. 4.19. From the voltage divider rule, the AC diode voltage v_{ d } is given by
v_{ d }=\frac{r_{ d }}{r_{ d }+R_{ L }} V_{ m } \sin \omega t (4.33)
=\frac{5.11}{5.11+1 k \Omega} 50 \times 10^{-3} \sin \omega t=0.2542 \times 10^{-3} \sin \omega t
Therefore, the instantaneous diode voltage v_{ D } is the sum of V_{ D } and v_{ d } . That is,
\begin{aligned}v_{ D } &=v_{ D }+v_{ d } \\&=0.7158+0.2542 \times 10^{-3} \sin \omega t V\end{aligned}

Related Answered Questions
The zener diode regulator for PSpice simulation is...
V_{ Z }=6.3 V \text { at } i_{ ZT }=40 mA ...
From Eq. (4.50), the junction power dissipation at...
(a) R_{ D }=50 \Omega, V_{ TD }=0.7 V , R...
V_{ S }=10 V , V_{ m }=50 mV , \text { and...
V_{ S }=15 V \text { and } R_{ L }=250 \Om...
V_{ Z }=4.7 V , P_{ Z (\max )}=400 mW , i_...
Using Eq. (4.37), we have
v_{ Z }=v_{ ZO }...
If input V_{ A } \text { or } V_{ B } [/la...
V_{ S }=10 V \text { and } R_{ L }=1 k \Om...