The source in Figure 8-57 has an internal source resistance of 75 Ω. Determine the load power for each of the following values of load resistance:
(a) 0 Ω (b) 25 Ω (c) 50 Ω (d) 75 Ω (e) 100 Ω (f) 125 Ω
Draw a graph showing the load power versus the load resistance.

Question

Accepted Answer

Use Ohm's law ([latex]I=V/R[/latex] ) and the power formula ([latex]P= I^{2}R[/latex]) to find the load power[latex]P_{L}[/latex],for each value of load resistance.

(a) For [latex]R_{L}[/latex]= 0 Ω.

[latex]I= \frac{V_{S}}{R_{S}+ R_{L}} = \frac{10 \ V}{75 \ \Omega + 0 \ \Omega } = 133 \ mA[/latex]

[latex]P_{L}= I^{2}R_{L}= (133 \ mA)^{2} (0 \ \Omega )= 0 \ mW[/latex]

(b) For [latex]R_{L}[/latex]= 25 Ω.

[latex]I= \frac{V_{S}}{R_{S}+ R_{L}} = \frac{10 \ V}{75 \ \Omega + 25 \ \Omega } = 100 \ mA[/latex]

[latex]P_{L}= I^{2}R_{L}= (100 \ mA)^{2} (25 \ \Omega )= 250 \ mW[/latex]

(C) For [latex]R_{L}[/latex]= 50 Ω.

[latex]I= \frac{V_{S}}{R_{S}+ R_{L}} = \frac{10 \ V}{ 125 \ \Omega } = 80 \ mA[/latex]

[latex]P_{L}= I^{2}R_{L}= (80 \ mA)^{2} (50 \ \Omega )= 320 \ mW[/latex]

(d) For [latex]R_{L}[/latex]= 75 Ω.

[latex]I= \frac{V_{S}}{R_{S}+ R_{L}} = \frac{10 \ V}{ 150 \ \Omega } = 66.7 \ mA[/latex]

[latex]P_{L}= I^{2}R_{L}= (66.7 \ mA)^{2} (75 \ \Omega )= 334\ mW[/latex]

(e) For [latex]R_{L}[/latex]= 100 Ω.

[latex]I= \frac{V_{S}}{R_{S}+ R_{L}} = \frac{10 \ V}{ 175 \ \Omega } = 57.1 \ mA[/latex]

[latex]P_{L}= I^{2}R_{L}= (57.1 \ mA)^{2} (100 \ \Omega )= 326\ mW[/latex]

(f) For [latex]R_{L}[/latex]= 125 Ω.

[latex]I= \frac{V_{S}}{R_{S}+ R_{L}} = \frac{10 \ V}{ 200 \ \Omega } = 50 \ mA[/latex]

[latex]P_{L}= I^{2}R_{L}= (50 \ mA)^{2} (125 \ \Omega )= 313\ mW[/latex]

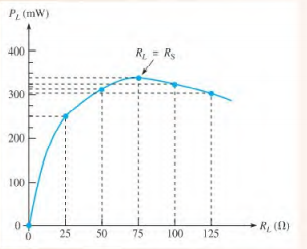
Notice that the load power is greatest when [latex]R_{L}[/latex]= 75 Ω, which is the same as the internal source resistance. When the load resistance is less than or greater than this value, the power drops off , as the curve in Figure 8-58 graphically illustrates.

Curve showing that the load power is maximum when [latex]R_{L}[/latex] = [latex]R_{S}[/latex]

Question 8.18: The source in Figure 8-57 has an internal source resistance ...

Related Answered Questions