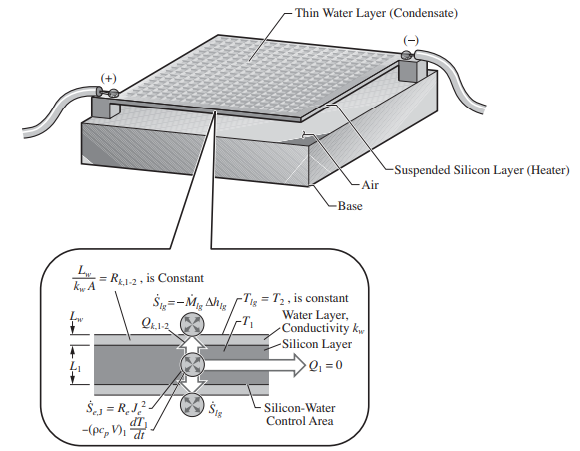
To detect the presence of water vapor in an otherwise pure air, a heatercondensate detector is used. The presence of the condensate on the heater results in a slower rise in the heater temperature, as compared to when there is no condensate present. The heater-detector, which is based on the Joule heating
of a silicon layer, is shown in Figure. A thin layer of water of thickness L_{w} is present on each side of the heater and the silicon-water contact area is A_{k} . The initial temperature of the silicon is T_{1}(t = 0) and suddenly a current J_{e} is passed through the silicon, which has an electrical resistance R_{e} . This resistance R_{e} is achieved by allowing for a matrix structure within the silicon layer (but is not shown). The heater is suspended such that the heat loss to the ambient, other than the condensate, is negligible.
(a) For a given water-layer surface temperature T_{2} = T_{lg} (at local vapor pressure pg), and for the parameters specified below, determine the elapsed time required for the heater temperature (assumed to be uniform, i.e., N_{k,1} < 0.1 ) to reach T_{1} = T_{lg} + 50^{\circ }C .
(b) Show that N_{k} < 0.1 , by using L1 for the silicon layer conduction length.
L_{w} = 0.1 mm , k_{w} (water) = 0.65 W/m-K , A_{k} = 10^{−4} cm^{2}, L_{1} = 1 mm, R_{e} = 10 ohm , J_{e} = 2 A, (ρc_{p} )_{1} = 1.6 × 10^{6} J/m^{3}-K, T_{1}(t = 0) = 5^{\circ}C, T_{2} = T_{lg} = 15^{\circ}C.
Note that using \tau _{1}=(\rho c_{p}V)_{1}R_{k,1-2}, a_{1}=\frac{\dot{S}_{1}-Q_{1}}{(\rho c_{p}V)_{1}} ,then Q_{1}+\frac{T_{1}-T_{2}}{R_{k,1-2}}=-\frac{d}{dt}(\rho c_{p}V)_{1}T_{1}+\dot{S}_{1} becomes
\frac{dT_{1}}{dt} +\frac{T_{1}-T_{2}}{\tau _{1}}=a_{1}With a_{1} = 0, this shows how T_{1} returns to thermal equilibrium value T_{2} during the relaxation period τ_{1}. Under steady-state, dT_{1}/dt = 0, and we have T_{1}(t → ∞) = T_{1} + a_{1}τ_{1}.