| Beam and Loading |
Elastic Curve |
Maximum Deflection |
Slope at End |
Equation of Elastic Curve |
 |
 |
−3EIPL3 |
−2EIPL2 |
y=6EIP(x3−3Lx2) |
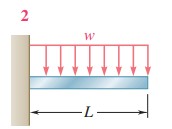 |
 |
−8EIwL4 |
−6EIwL3 |
y=24EIw(x4−4Lx3+6L2x2) |
 |
 |
−2EIML2 |
−EIML |
y=−2EIMx2 |
 |
 |
−48EIPL3 |
±16EIPL2 |
For x≤21L:
y=48EIP(4x3−3L2x) |
 |
 |
For a > b:
−93EILPb(L2−b2)3/2
|
θA=−6EILPb(L2−b2)
|
For x<a:
y=6EILPb[x3−(L2−b2)x]
|
| at xm=3L2−b2 |
θB=+6EILPa(L2−a2) |
For x = a:
y=−3EILPa2b2 |
 |
 |
−384EI5wL4 |
±24EIwL3 |
y=−24EIw(x4−2Lx3+L3x) |
 |
 |
93EIML2 |
θA=+6EIML |
y=−6EILM(x3−L2x) |
| θB=−3EIML |














