Question 11.4: A brass bar AB projecting from the side of a large machine i......
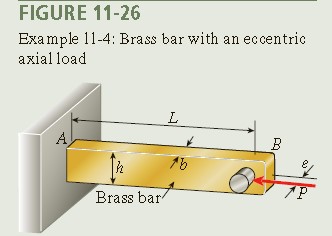
A brass bar AB projecting from the side of a large machine is loaded at end B by a force P = 7 kN acting with an eccentricity e = 11 mm (Fig. 11-26). The bar has a rectangular cross section with height h = 30 mm and width b = 15 mm.
What is the longest permissible length L_{max} of the bar if the deflection at the end is limited to 3 mm? (For the brass, use E = 110 GPa.)
Learn more on how do we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize:
Critical load: This bar is a slender column that is fixed at end A and free at end B. Therefore, the critical load (see Fig. 11-20b) is
\quad\quad\quad\quad P_{cr}=\frac{\pi^{2}E{{{I}}}}{4L^{2}}\quad\quad(a)
The moment of inertia for the axis about which bending occurs is
\quad\quad\quad\quad I={\frac{h b^{3}}{12}}={\frac{(3{0}\operatorname*{mm})(15\operatorname*{mm})^{3}}{12}}=8.44\times10^{3}{mm}^{4}
Therefore, the expression for the critical load becomes
\quad\quad\quad\quad P_{cr}=\frac{\pi^{2}(110~{\mathrm{GPa}})(8.44\times10^{3}\ \,\mathrm{mm}^{4})}{4L^{2}}=\frac{2.29\,\mathrm{kN}\cdot\mathrm{m}^{2}}{L^{2}}\quad\quad (b)
in which P_{cr} has units of kN and L has units of meters.
2. Categorize:
Deflection: The deflection at the end of the bar is given by Eq. (11-62), which applies to a fixed-free column as well as a pinned-end column:
\quad\quad\quad\quad \delta=e\left[\sec {\Bigg\lgroup}{\frac{\pi}{2}}{\sqrt{\frac{P}{P_{\mathrm{cr}}}}}{\Bigg\rgroup}-1\right]\quad\quad (c)
In this equation, P_{cr} is given by Eq. (a).
3. Analyze:
Length: To find the maximum permissible length of the bar, substitute for \delta its limiting value of 3 mm. Also, substitute e = 11 mm and P = 7 kN, and substitute for P_{cr} from Eq. (b). Thus,
\quad\quad\quad\quad 3~mm = (1~mm)\begin{bmatrix} sec{\Bigg\lgroup}\frac{\pi}{2}\sqrt{\frac{7~kN}{2.29/L^2}}{\Bigg\rgroup} – 1 \end{bmatrix}
The only unknown in this equation is the length L (meters). To solve for L, perform the various arithmetic operations in the equation and then rearrange the terms. The result is
\quad\quad\quad\quad 0.2727 = sec(2.746L) – 1
Use radians and solve this equation to get L = 0.243 m. Thus, the maximum permissible length of the bar is
\quad\quad\quad\quad L_{max} = 0.243 m
4. Finalize: If a longer bar is used, the deflection will exceed the allowable value of 3 mm.
