Question 11.10: Planar motion: mass hanging from a pulley A circular pulley ...
Planar motion: mass hanging from a pulley
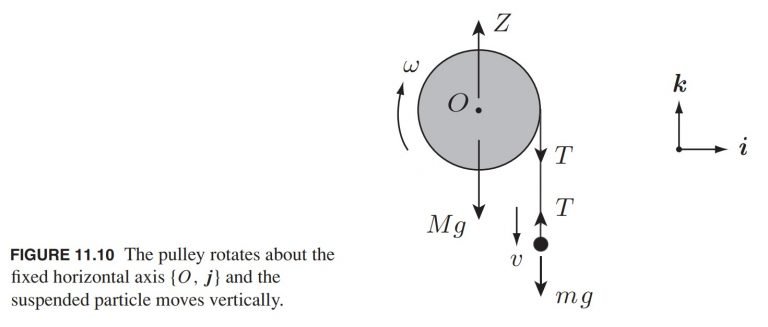
A circular pulley of mass M and radius a is smoothly pivoted about the axis {O, j}, as shown in Figure 11.10. A light inextensible string is wrapped round the pulley so that it does not slip, and a particle of mass m is suspended from the free end. The system undergoes planar motion with the particle moving vertically. Find the downward acceleration of the particle.
Learn more on how we answer questions.
This problem is most easily solved by using energy conservation, but it is instructive to solve it as a planar motion problem to illustrate the difference between the two approaches. In the energy conservation approach, the whole system is considered to be a single entity, and in this case, the string tensions do no total work and need not be considered. In the setting of planar motion however, the system consists of two elements, (i) a particle moving in a vertical straight line, and (ii) a rigid pulley rotating about a fixed horizontal axis. For each constituent, the tension force exerted by the string is external. The string tensions (which are equal in this problem) therefore appear in the equations of motion. For this reason, the conservation method is simpler, but there are many problems where there is no useful conservation principle and the planar motion approach is essential.
Let the particle have downward vertical velocity v, and the pulley have angular velocity ω (in the sense shown) at time t. Since the vector j points into the page, this is the positive sense around the axis {O, j}. Thus, in the notation used here, the positive sense for angular velocity is clockwise. The same applies to moments and angular momenta.
First consider the motion of the particle. Since the motion is in a vertical straight line, the only surviving euation is
m \frac{d v}{d t}=m g-T,
where T is the string tension at time t.
Now consider the motion of the pulley. Since this is rotating about a fixed axis, the equation of motion is I_{O} d \omega / d t=K_{O}, that is,
I_{O} \frac{d \omega}{d t}=a T,
since the weight force Mg and the pivot reaction Z have zero moment about O.
Hence, the unknown tension T can be eliminated to give
\left(m a \frac{d v}{d t}+I_{O} \frac{d \omega}{d t}\right)=m g a.
This equation applies whether or not the string slips on the pulley. However, since we are given that the string does not slip, v and ω must be related by the no-slip condition v = ωa. On using this condition in the last equation, we obtain
\frac{d v}{d t}=\left(\frac{m a^{2}}{m a^{2}+I_{O}}\right) g.
This is the downward acceleration of the particle. If the moment of inertia of the pulley is \frac{1}{2} M a^{2}, then the value of this acceleration is [2m/(2m + M)]g.