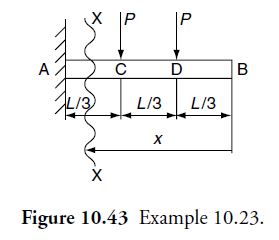
Question 10.23: Find δC , δD , δC of the cantilever beam shown in Figure 10....
Find \delta_C, \delta_D, \delta_C of the cantilever beam shown in Figure 10.43.
Learn more on how we answer questions.
Clearly, bending moment at any section at a distance x from end B is given by
M_x=\left\{\begin{array}{ll} 0 ; & 0 \leq x \leq L / 3 \\ -P_1\left\lgroup x-\frac{L}{3} \right\rgroup ; & L / 3 \leq x \leq 2 L / 3 \\ -P_2\left\lgroup x-\frac{2 L}{3} \right\rgroup -P_1\left\lgroup x-\frac{L}{3} \right\rgroup ; & 2 L / 3 \leq x \leq L \end{array}\right\}
\text { where } P_1=P_2=P_1 \text { (let) and } P_{ D }=P_1, P_{ C }=P_2 . Therefore,
U=\left\lgroup \frac{1}{2 E I} \right\rgroup \int_0^L M_x^2 d x
or U=\left\lgroup \frac{1}{2 E I} \right\rgroup \left[\int_{L / 3}^{2 L / 3} M_x^2 d x+\int_{2 L / 3}^L M_x^2 d x\right] (1)
Differentiating under integral sign using Leibneitz’s rule, we get
\frac{\partial U}{\partial P_1}=\left\lgroup \frac{1}{E I} \right\rgroup \left[\int_{L / 3}^{2 L / 3} M_x \frac{\partial M_x}{\partial P_1} d x+\int_{2 L / 3}^L M_x \frac{\partial M_x}{\partial P_1} d x\right]
=\left\lgroup \frac{1}{E I} \right\rgroup\left\{\int_{L / 3}^{2 L / 3} P_1\left\lgroup x-\frac{L}{3} \right\rgroup^2 d x+\int_{2 L / 3}^L\left\lgroup x-\frac{L}{3} \right\rgroup\left[P_1\left\lgroup x-\frac{L}{3} \right\rgroup +P_2\left\lgroup x-\frac{2 L}{3} \right\rgroup\right] d x\right\}
Therefore,
\frac{\partial U}{\partial P_1}=\left\lgroup \frac{1}{E I} \right\rgroup\left\{\left[\frac{P_1}{3}\left\lgroup x-\frac{L}{3} \right\rgroup^3\right]_{L / 3}^{2 L / 3}+\left[\frac{P_1}{3}\left\lgroup x-\frac{L}{3} \right\rgroup^3+P_2\left\lgroup \frac{x^3}{3}-\frac{L x^2}{2}+\frac{2 L^2}{9} x \right\rgroup\right]_{2 L / 3}^L\right\}
=\frac{1}{E I}\left\lgroup \frac{P_1 L^3}{81}+\frac{8 P_1 L^3}{81}+\frac{P_2 L^3}{18}-\frac{P_1 L^3}{81}-\frac{2 P_2 L^3}{81} \right\rgroup
=\frac{1}{E I}\left[\frac{8 P_1 L^3}{81}+\frac{5 P_2 L^3}{(81)(2)}\right]
By Castigliano’s second theorem
\delta_{ D }=\underset{\substack{P_1 \rightarrow P \\ P_2 \rightarrow P}}{Lt } \frac{\partial U}{\partial P_1}=\underset{\substack{P_1 \rightarrow P \\ P_2 \rightarrow P}}{Lt } \frac{1}{E I}\left[\frac{16 P_1 L^3}{162}+\frac{5 P_2 L^3}{162}\right]
or \delta_{ D }=\frac{21 P L^3}{162 E I}=\frac{7 P L^3}{54 E I}
Therefore,
\delta_{ D }=\frac{7 P L^3}{54 E I}(\downarrow)
Again from Eq. (1) above
\frac{\partial U}{\partial P_2}=\left\lgroup \frac{1}{E I} \right\rgroup\left[\int_{L / 3}^{2 L / 3} M_x \frac{\partial M_x}{\partial P_2} d x+\int_{2 L / 3}^L M_x \frac{\partial M_x}{\partial P_2} d x\right]
or \frac{\partial U}{\partial P_2}=\left\lgroup \frac{1}{E I} \right\rgroup\left\{\int_{L / 3}^{2 L / 3}-P_1\left\lgroup x-\frac{L}{3} \right\rgroup \cdot 0 d x+\int_{2 L / 3}^L\left[P_2\left\lgroup x-\frac{2 L}{3} \right\rgroup^2+P_1\left\lgroup x-\frac{L}{3} \right\rgroup\left\lgroup x-\frac{2 L}{3} \right\rgroup\right] d x\right\}
=\left\lgroup \frac{1}{E I} \right\rgroup\left[\frac{P_2\left\lgroup x-\frac{2 L}{3} \right\rgroup ^3}{3}+P_1\left\lgroup \frac{x^3}{3}-\frac{L x^2}{2}+\frac{2 L^2 x}{9} \right\rgroup\right]_{2 L / 3}^L
=\left\lgroup =\frac{1}{E I} \right\rgroup\left[\frac{P_2 L^3}{81}+\frac{P_1 L^3}{18}-\frac{2 P_2 L^3}{81}\right]
=\left\lgroup \frac{1}{E I} \right\rgroup \left[\frac{P_1 L^3}{18}-\frac{P_2 L^3}{81}\right]=\frac{L^3}{162 E I}\left(9 P_1-2 P_2\right)
Therefore,
\delta_{ C }=\underset{\substack{P_1 \rightarrow P \\ P_2 \rightarrow P}}{Lt }\left\lgroup \frac{\partial U}{\partial P_2} \right\rgroup
or \delta_{ C }=\frac{7 P L^3}{162 E I}(\downarrow)
To find \delta_{ B } , we note there is no generalised force acting on the structure and hence we put a dummy load Q at B and calculate the strain energy of the beam (Figure 10.44). The bending moment, M_x of the beam at any distance x from free end of the beam is
M_x=\left\{\begin{array}{lrl} -Q x ; & & 0 \leq x \leq \frac{L}{3} \\ -P\left\lgroup x-\frac{L}{3} \right\rgroup-Q x ; & & \frac{L}{3} \leq x \leq \frac{2 L}{3} \\ -P\left\lgroup x-\frac{2 L}{3} \right\rgroup -P\left\lgroup x-\frac{L}{3} \right\rgroup -Q x ; & \frac{2 L}{3} & \leq x \leq L \end{array}\right\}
Therefore,
U=\left\lgroup \frac{1}{2 E I} \right\rgroup \int_0^L M_x^2 d x
=\left\lgroup\frac{1}{2 E I} \right\rgroup \left[\int_0^{L / 3} M_x^2 d x+\int_{L / 3}^{2 L / 3} M_x^2 d x+\int_{2 L / 3}^L M_x^2 d x\right]
Differentiating with respect to Q, we get
\frac{\partial U}{\partial Q}=\left\lgroup\frac{1}{E I} \right\rgroup\left[\int_0^{L / 3} M_x\left\lgroup\frac{\partial M_x}{\partial Q} \right\rgroup d x+\int_{L / 3}^{2 L / 3} M_x\left\lgroup\frac{\partial M_x}{\partial Q} \right\rgroup d x+\int_{2 L / 3}^L M_x\left\lgroup\frac{\partial M_x}{\partial Q} \right\rgroup d x\right]
=\left\lgroup\frac{1}{E I} \right\rgroup \left\{\int_0^{L / 3} Q x^2 d x+\int_{L / 3}^{2 L / 3}\left[P\left\lgroup x^2-\frac{L x}{3} \right\rgroup+Q x^2\right] d x+\int_{2 L / 3}^L\left[P\left(2 x^2-x L\right)+Q x^2\right] d x\right\}
Now, by Castigliano’s second theorem
\delta_{ B }=\underset{Q \rightarrow 0}{Lt}\left\lgroup \frac{\partial U}{\partial Q} \right\rgroup
=\frac{1}{E I}\left[\int_{L / 3}^{2 L / 3} P\left\lgroup x^2-\frac{L x}{3} \right\rgroup d x+\int_{2 L / 3}^L P\left(2 x^2-x L\right) d x\right]
Thus,
\delta_{ B }=\left\lgroup \frac{1}{E I} \right\rgroup\left\{P\left[\frac{x^3}{3}-\frac{L x^2}{6}\right]_{L / 3}^{2 L / 3}+\left[P\left\lgroup \frac{2 x^3}{3}-\frac{x^2 L}{2} \right\rgroup\right]_{2 L / 3}^L\right\}
=\left\lgroup \frac{1}{E I} \right\rgroup \left[P\left\lgroup \frac{8 L^3}{81}-\frac{2 L^3}{27}-\frac{L^3}{81}+\frac{L^3}{54} \right\rgroup +P\left\lgroup \frac{2 L^3}{3}-\frac{L^3}{2}-\frac{16 L^3}{81}+\frac{2 L^3}{9} \right\rgroup \right]
=\left\lgroup \frac{1}{E I} \right\rgroup \left\lgroup \frac{5 P L^3}{162}+\frac{31 P L^3}{162} \right\rgroup =\frac{36 P L^3}{162 E I}=\frac{2 P L^3}{9 E I}
Thus, \delta_{ B }=\frac{2 P L^3}{9 E I}(\downarrow)
