Question 10.10: Using VSEPR Theory to Predict a Geometric Shape Predict the ...

Step 1. Write the Lewis structure. The number of valence electrons is

\begin{matrix} \text{From I} & \text{From Cl} & \text{To establish ionic charge of } -1 & \\ (1 \times 7) & (4 \times 7)  + & 1 & = 36\end{matrix}

To join 4 Cl atoms to the central I atom and to provide octets for all the atoms, we need 32 electrons. In order to account for all 36 valence electrons, we need to place an additional four electrons around the I atom as lone pairs. That is, we are forced to expand the valence shell of the I atom to accommodate all the electrons required in the Lewis structure.

\left[\begin{array}{r c}\begin{matrix} \ \text{:}\underset{\cdot \cdot}{\ddot{Cl} } \ _{_\diagdown }\quad\quad\quad _{_\diagup }\underset{\cdot \cdot}{\ddot{Cl} }\text{:} \\\text{:I:}\\ \text{:}\underset{\cdot \cdot}{\ddot{Cl} }\ ^{^\diagup }\quad \quad \ \ ^{^\diagdown }\underset{\cdot \cdot}{\ddot{Cl} }\text{:} \\ \\ \end{matrix} \end{array} \right]^-

Step 2. There are six electron groups around the I atom, four bond pairs and two lone pairs.

Step 3. The electron-group geometry (the orientation of six electron groups) is octahedral.

Step 4. The ICl_4{ }^- anion is of the type A {\chi} _4 E_2,  which according to Table 10.1, leads to a molecular geometry that is square planar.

TABLE 10.1 Molecular Geometry as a Function of Electron-Group Geometry
Number of Electron Groups	Electron-Group Geometry	Number of Lone Pairs	VSEPR Notation	Molecular Geometry	Ideal Bond Angles	Example
2	linear	0	A \chi_2		180°	BeCl_2
3	trigonal planar	0	A \chi_3		120°	BF_3
	trigonal planar	1	A \chi_2 E		120°	SO_2{ }^a
4	tetrahedral	0	A \chi_4		109.5°	CH_4
	tetrahedral	1	A \chi_3 E		109.5°	NH_3
	tetrahedral	2	A \chi_2 E_2		109.5°	OH_2
5	trigonal bipyramidal	0	A \chi_5		90°,120°	PCl_5
	trigonal bipyramidal	1	A \chi_4 E^b		90°,120°	SF_4
	trigonal bipyramidal	2	A \chi_3 E_2		90°	ClF_3
	trigonal bipyramidal	3	A \chi_2 E_3		180°	\chi eF_2
6	octahedral	0	A \chi_6		90°	SF_6
	octahedral	1	A \chi_5 E		90°	BrF_5
	octahedral	2	A \chi_4 E_2		90°	\chi eF_4

_{}^{a}\textrm{For }a discussion of the structure of SO_2, see page 428.
_{}^{b}\textrm{For }a discussion of the placement of the lone-pair electrons in this structure, see page 427.

Assess
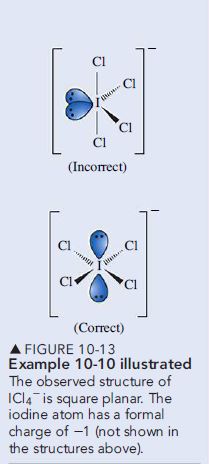
Figure 10-13 suggests two possibilities for distributing bond pairs and lone pairs in ICl_4{ }^-. The square planar structure is correct because the lone pair lone pair interaction is kept at 180°. In the incorrect structure, this interaction is at 90°. which results in a strong repulsion.