Question 10.13: Determining the Relationship Between Geometric Shapes and th...

Polar: $ICl, NO, SO_2 .$ ICl and NO are diatomic molecules with an electronegativity difference between the bonded atoms. $SO_2$ is a bent molecule with an electronegativity difference between the S and O atoms.
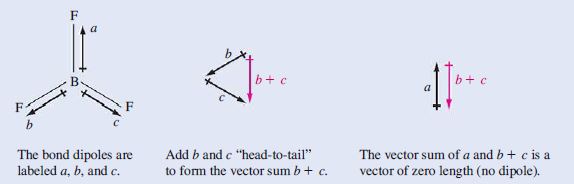
Nonpolar: $Cl_2$ and $BF_3$. $Cl_2$ is a diatomic molecule of identical atoms; hence no electronegativity difference. For $BF_3$, refer to Table 10.1. $BF_3$ is a symmetrical planar molecule (120° bond angles). The $\begin{matrix} B-F \end{matrix}$ bond dipoles cancel each other.

TABLE 10.1 Molecular Geometry as a Function of Electron-Group Geometry
Number of Electron Groups	Electron-Group Geometry	Number of Lone Pairs	VSEPR Notation	Molecular Geometry	Ideal Bond Angles	Example
2	linear	0	$A \chi_2$		180°	$BeCl_2$
3	trigonal planar	0	$A \chi_3$		120°	$BF_3$
	trigonal planar	1	$A \chi_2 E$		120°	$SO_2{ }^a$
4	tetrahedral	0	$A \chi_4$		109.5°	$CH_4$
	tetrahedral	1	$A \chi_3 E$		109.5°	$NH_3$
	tetrahedral	2	$A \chi_2 E_2$		109.5°	$OH_2$
5	trigonal bipyramidal	0	$A \chi_5$		90°,120°	$PCl_5$
	trigonal bipyramidal	1	$A \chi_4 E^b$		90°,120°	$SF_4$
	trigonal bipyramidal	2	$A \chi_3 E_2$		90°	$ClF_3$
	trigonal bipyramidal	3	$A \chi_2 E_3$		180°	$\chi eF_2$
6	octahedral	0	$A \chi_6$		90°	$SF_6$
	octahedral	1	$A \chi_5 E$		90°	$BrF_5$
	octahedral	2	$A \chi_4 E_2$		90°	$\chi eF_4$

$_{}^{a}\textrm{For }$a discussion of the structure of $SO_2$, see page 428.
$_{}^{b}\textrm{For }$a discussion of the placement of the lone-pair electrons in this structure, see page 427.

Assess
Bond dipoles are vector quantities. When adding them together, we must add them as vectors, that is, “head-to-tail,” as illustrated below.