Question 25.3: Using the Half-Life Concept and the Radioactive Decay Law to...
Using the Half-Life Concept and the Radioactive Decay Law to Describe the Rate of Radioactive Decay
The phosphorus isotope _{}^{32}\text{P} is used in biochemical studies to determine the pathways of phosphorus atoms in living organisms. Its presence is detected through its emission of \beta^- particles. (a) What is the decay constant for _{}^{32}\text{P}, expressed in the unit s^{-1}? (b) What is the activity of a 1.00 mg sample of _{}^{32}\text{P} (that is, how many atoms disintegrate per second)? (c) Approximately what mass of _{}^{32}\text{P} will remain in the original 1.00 mg sample after 57 days? (See Table 25.1.) (d) What will be the rate of radioactive decay after 57 days?
Analyze
To solve these types of problems, we need to determine the decay constant, λ, of the radioactive species, which is related to the concept of half-life through equation (25.13). After determining the decay constant from the half-life of the sample, we can then use it to determine the activity for part (b).
t_{1 / 2}=\frac{0.693}{\lambda} (25.13)
| TABLE 25.1 Some Representative Half-Lives | |||||
| Nuclide | \text{Half-Life}^a | Nuclide | \text{Half-Life}^a | Nuclide | \text{Half-Life}^a |
| _{1}^{3}\text{H} | 12.26 y | _{19}^{40}\text{K} | 1.25 \times 10^9 y | _{84}^{214}\text{Po} | 1.64 \times 10^{-4} s |
| _{6}^{14}\text{C} | 5730 y | _{35}^{80}\text{Br} | 17.6 min | _{86}^{222}\text{Rn} | 3.823 d |
| _{8}^{13}\text{O} | 8.7 \times 10^{-3} s | _{38}^{90}\text{Sr} | 27.7 y | _{88}^{226}\text{Ra} | 1.60 × 10³ y |
| _{12}^{28}\text{Mg} | 21 h | _{53}^{131}\text{I} | 8.040 d | _{90}^{234}\text{Th} | 24.1 d |
| _{15}^{32}\text{P} | 14.3 d | _{55}^{137}\text{Cs} | 30.23 y | _{92}^{238}\text{U} | 4.51 \times 10^9 y |
| _{16}^{35}\text{S} | 88 d | ||||
_{}^{a}\text{s}, second; min, minute; h, hour; d, day; y, year.
Learn more on how we answer questions.
(a) We can determine λ from t_{1/2} with equation (25.13). The first result we get has the unit d^{-1}. We must convert this unit to h^{-1}, \text{min}^{-1}, and s^{-1}.
\lambda=\frac{0.693}{14.3 d } \times \frac{1 d }{24 h } \times \frac{1 h }{60 min } \times \frac{1 min }{60 s }=5.61 \times 10^{-7} s ^{-1}
(b) First, let us find the number of atoms, N, in 1.00 mg of _{}^{32}\text{P}.
N\left({ }^{32} \text{P} \text { atoms}\right) = 0.00100 g \times \frac{1 \text{ mol } _{}^{32} \text{P} }{32.0 g } \times \frac{6.022 \times 10^{23}\text{ } _{}^{32} \text{P} \text { atoms }}{1 \text{mol} _{}^{32} \text{P} }
=1.88 \times 10^{19} \text{ } _{}^{32} \text{P} \text { atoms }
Then, we can multiply this number by the decay constant to get the activity or decay rate.
\text { activity }=\lambda N=5.61 \times 10^{-7} s ^{-1} \times 1.88 \times 10^{19} \text { atoms }
= 1.05 \times 10^{13} \text{ atomes/s}
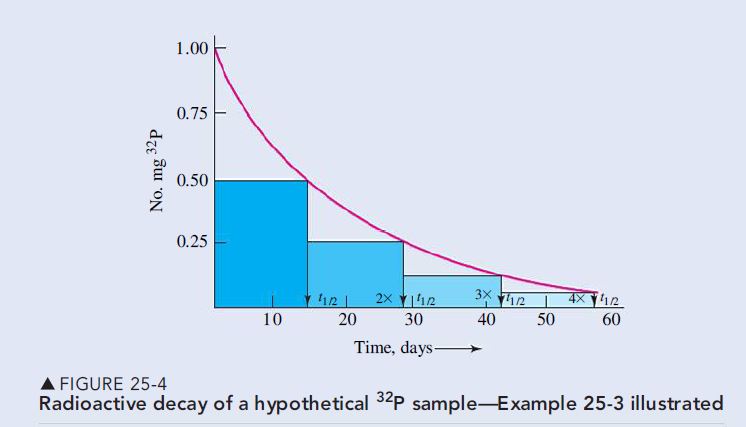
(c) A period of 57 days is 57/14.3 = 4.0 half-lives. As shown in Figure 25-4, the quantity of radioactive material decreases by one-half for every half-life. The quantity remaining is (\frac{1}{2})^4 of the original quantity.
? \text{mg} \text{ } _{}^{32} \text{P} =1.00 \text{mg} \times \left(\frac{1}{2} \right)^4 = 1.00 \text{mg} \times \frac{1}{16}=0.063 \text{mg} \text{ } _{}^{32} \text{P}
(d) The activity is directly proportional to the number of radioactive atoms remaining (activity = λN), and the number of atoms is directly proportional to the mass of _{}^{32}\text{P}. When the mass of _{}^{32}\text{P} has dropped to one-sixteenth its original mass, the number of _{}^{32}\text{P} atoms also falls to one-sixteenth the original number, and the rate of decay is one-sixteenth the original activity.
\text { rate of decay }=\frac{1}{16} \times 1.05 \times 10^{13} \text { atoms/s} =6.56 \times 10^{11} \text { atoms/s}
Assess
Phosphorus-32 isotope is an ideal radionuclide to use because of its short half-life. This time is long enough to carry out experiments, yet short enough that disposal is not a major problem. We see in this example that after 57 days, approximately 6% of the original mass of phosphorus remains.