Question 6.11: A doubly symmetric hollow box beam (Fig. 6-55) of elastoplas......
A doubly symmetric hollow box beam (Fig. 6-55) of elastoplastic material (σ_Y = 220 ~MPa) is subjected to a bending moment M of such magnitude that the flanges yield but the webs remain linearly elastic.
Determine the magnitude of the moment M if the dimensions of the cross section are b = 150~ mm, b_1 = 130 ~mm, h = 200~ mm, ~and ~ h_1 = 160 ~~mm.

Learn more on how do we answer questions.
Use a four-step problem-solving approach. Combine steps as needed for an efficient solution.
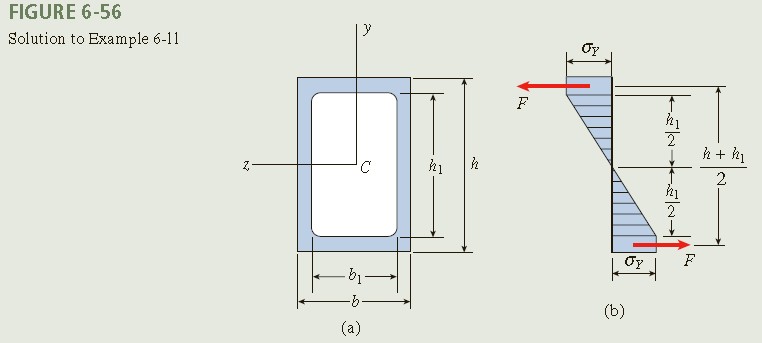
1, 2. Conceptualize, Categorize: The cross section of the beam and the distribution of the normal stresses are shown in Figs. 6-56a and b, respectively. From the figure, note that the stresses in the webs increase linearly with distance from the neutral axis and the stresses in the flanges equal the yield stress σ_Y. Therefore, the bending moment M acting on the cross section consists of two parts:
(i) A moment M_1 corresponding to the elastic core.
(ii) A moment M_2 produced by the yield stresses σ_Y in the flanges.
3. Analyze: The bending moment supplied by the core is found from the flexure formula [Eq. (6-87)] with the section modulus calculated for the webs alone; thus,
\quad\quad\quad M_{Y}\,=\,\frac{\sigma_{Y}I}{c}\,=\,{\sigma_{Y}{S}} \quad\quad (6-87)
\quad\quad\quad S_{1}={\frac{(b-b_{1})h_{1}^{2}}{6}}\quad\quad (6-111)
and
\quad\quad\quad M_{1}=\sigma_{Y}S_{1}=\frac{\sigma_{Y}(b-b_{1})h_{1}^{2}}{6}\quad\quad (6-112)
To find the moment supplied by the flanges, note that the resultant force F in each flange (Fig. 6-56b) is equal to the yield stress multiplied by the area of the flange:
\quad\quad\quad F=\sigma_{Y}b\!{\Bigg\lgroup} \frac{h – h_{1}}{2} {\Bigg\rgroup}\quad\quad\quad\quad (a)
The force in the top flange is compressive, and the force in the bottom flange is tensile if the bending moment M is positive. Together, the two forces create the bending moment M_2:
\quad\quad\quad {M}_{2}=F{\Bigg\lgroup} \frac{h+h_{1}}{2} {\Bigg\rgroup} =\frac{\sigma_{Y}b(h^{2}-h_{1}^{2})}{4}\quad\quad (6-113)
Therefore, the total moment acting on the cross section, after some rearranging, is
\quad\quad\quad {M}=M_{1}+M_{2}=\frac{\sigma_{Y}}{12}\Big[3b h^{2}-(b+2b_{1})h_{1}^{2}\Big]\quad\quad (6-114)
Substitute the given numerical values to obtain
\quad\quad\quad M = 138 \mathrm{kN}\cdot\mathrm{m}
4. Finalize: Note: The yield moment M_Y and the plastic moment M_P for the beam in this example have the following values (determined in Prob. 6.10-13):
\quad\quad\quad M_{Y}\,=\,122\,\mathrm{kN}\cdot\mathrm{m}\quad M_{P}\,=\,\mathrm{l}47\,\mathrm{kN}\cdot\mathrm{m}
The bending moment M is between these values, as expected.